El campo electromagnético es quizás la primera pesadilla de cualquier estudiante de física ya en el instituto. Personalmente en aquélla etapa siempre lo encontré horripilante. El motivo, muy en contra de lo que pudiera parecer, no es que sea esencialmente difícil de comprender, sino que su naturaleza tiene una complejidad matemática tal que cualquier forma de simplificar su explicación para alumnos de instituto lo convierte en un ente bastante feo y formalmente amorfo. Por ese motivo, he retrasado todo lo que he podido su aparición en este blog hasta poder plantearlo de un modo que no se antoje tan poco atractivo.

Introducción:

En esta entrada comentaré las ideas esenciales de este campo, responsable de la mayor parte de las cosas que vivimos en el día a día como empujar una mesa, encender un televisor o incluso ver, y para darle mayor interés lo haré partiendo de donde nunca he visto ni leído a nadie hacerlo, desde la teoría de la relatividad especial.

La teoría electromagnética, de la cual se dedujo el valor absoluto de la velocidad de la luz c, fue clave para que a Einstein se le ocurriese suponerla, además, la velocidad máxima del universo. Gracias a la teoría de la relatividad, además, se empezó a considerar el tiempo como una coordenada más a tener en cuenta junto a las espaciales, convirtiendo los vectores de posición en cuadrivectores de cuadriposición (el tiempo y 3 coordenadas espaciales). Asimismo, esto nos permitía redefinir el concepto de distancia con la métrica de Minkowski, según la cual el tiempo sumaría con un signo al calcular la distancia entre dos eventos espaciotemporales, y el espacio con el signo opuesto:

Definida toda esta nueva teoría, que rompía fundamentalmente en la física clásica con el límite máximo de velocidad y considerando 4 dimensiones, fue posible reformular el campo electromagnético que le había dado origen de un modo mucho más elegante que como lo dejaron escrito Maxwell y demás gente en el siglo XIX. Así pues, como voy a explicar el campo desde este nuevo enfoque en el que ya conocemos la relatividad anteriormente, es importante aclarar que no fue así ni de lejos como se planteó todo originalmente. Nosotros partiremos de la meta, y aunque os perdáis algo por el camino, de este modo el lector entenderá más electromagnetismo que los estudiantes de primeros años de carrera que no conocen este modo de enfocarlo.

Cuadripotencial:

El principal motivo por el que este campo es mucho más extraño que el gravitatorio de Newton es porque mientras que el potencial gravitatorio (y el elástico) eran funciones del espacio de las cuales se derivaba el campo como un gradiente según la teoría de campos, en este caso el potencial tiene una forma funcional V de mostrarse que muchos conoceréis como el responsable de la ley de Coulomb de atracción entre dos cargas, mientras que también se puede mostrar con otra forma vectorial a complicando las cosas. ¿Y cómo puede ser que un potencial sea un vector cuando desde siempre la energía y el potencial eran escalares? Pues parece ser que no eran tan escalares, y de hecho la existencia del potencial vector a es la responsable de la dificultad matemática del campo.

Así pues, comenzaremos definiendo el cuadripotencial electromagnético A con ayuda de las herramientas relativistas en su versión contravariante:

, donde dividimos v entre la velocidad de la luz en el vacío c por una correspondencia de unidades, del mismo modo que en relatividad dividimos en el tensor energía-momento la energía. Si queremos este cuadrivector en su versión covariante, simplemente tenemos que considerar la métrica de Minkowski que cambia de signo las componentes de a:

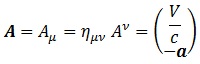Llegados a este punto, es importante recalcar que cuando escriba el índice 0 me referiré a la primera componente del cuadrivector, y cuando escriba 1,2,3 me referiré a las coordenadas espaciales rectangulares x,y,z.

Tensor de Faraday:

Definido ya el cuadripotencial, podemos definir el campo. El campo electromagnético, a diferencia del gravitatorio, tiene una forma tensorial en la que únicamente hay 6 componentes independientes, que son las 3 componentes de los campos eléctrico E y magnético B. Aunque Faraday, en su ignorancia matemática, nunca llegó a conocer la forma tensorial del campo, quienes lo formularon así décadas después decidieron ponerle su nombre, por ser él el primero en considerar que la electricidad debía de poderse describir con ayuda de dos «entes» que en cada punto del espacio tuviesen 3 componentes. Veamos pues, cómo se define el tensor F:

, donde. Es importante indicar que la primera componente μ determina las columnas del tensor y ν las filas. Por otra banda, es crucial el hecho de que F sea antisimétrico en tanto que al intercambiar sus índices el resultado cambia de signo. Esto es evidente si tenemos en cuenta que la forma de obtenerlo ha sido ya propiamente antisimétrica: la derivada μ de la componente ν menos la derivada ν de la componente μ del cuadripotencial.

Gracias a esta definición, además, podemos definir ya los vectores de campo E y B considerando cómo han aparecido:

El campo eléctrico E surge como oposición al gradiente del potencial V y a la variación temporal del potencial vector a. Debido a ello es un campo que puede ser a la vez radial por derivar de un gradiente (existen manantiales y sumideros de E) y también solenoide por derivar de un potencial vector (las líneas de E no son rectas sino que se pueden curvar). Técnicamente, estas conclusiones a las que he llegado exigen que la divergencia de a se anule para ser ciertas. Por último, hay que comentar que si a fuese nulo (como sucede en varios casos), el campo eléctrico sería conservativo y se podría definir mucho más fácilmente en su versión electrostática (no solenoide).

Por otra parte, el campo magnético B surge como el rotacional del potencial vector a, sin guardar ningún tipo de relación con V, ¡por lo que cuando el campo es electrostático no existe parte magnética! Por el mismo argumento que sucedía con E, este campo será solenoide siempre que exista (las líneas de B se curvan y se cierran sobre sí mismas, es decir, son cerradas).

Las conclusiones más importantes que debemos extraer de aquí son, en resumen, que B es un campo residual debido a la existencia de a, y que puede desaparecer perfectamente aún existiendo E. E es el campo predilecto del electromagnetismo, y de hecho lo es hasta un extremo que veremos posteriormente. Intuitivamente, uno ya puede observar en F que las unidades de E (Voltios/metro) se relacionan con las de B (Teslas) al dividirlas entre la velocidad de la luz en el vacío, lo que nos da una idea de la relación entre ambos campos y la velocidad, y nos recuerda que estamos construyendo todo esto así a partir de la relatividad.

Para concluir este apartado, obtendremos las formas co/contravariante y contravariante de F, empleando para ello una vez más la métrica de Minkowski:

Ecuaciones de Maxwell:

Pese a que ya tenemos 3 ecuaciones con las que describir nuestro campo: la nulidad de la divergencia de a, y las definiciones de E y B, ninguna de ellas fueron la base experimental sobre la que se construyó todo, sino que fueron las ecuaciones de Maxwell, que vienen a representar para el electromagnetismo lo que las leyes de Newton representaron para la mecánica clásica. Estas 4 ecuaciones, que se dedujeron una a una a partir de experimentos, en su versión tensorial tan sólo ocupan 2 líneas.

La primera ecuación tensorial de índole experimental (no se puede deducir) nos dice que el gradiente de F es igual al cuadrivector J de fuentes de campo:

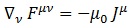, donde μ0 es la que se conoce como permeabilidad magnética del vacío y las componentes del cuadrivector J se definen acorde con el experimento:

, donde ρ es la densidad de carga en el punto del espacio a considerar y el vector j la densidad superficial de corriente eléctrica. En resumen:

Asimismo, con la definición de este cuadrivector de fuentes obtenemos las que se conocen como las 2 ecuaciones inhomogéneas (por la presencia de J) de Maxwell:

.-La Ley de Gauss nos dice que la divergencia de E es proporcional a la densidad de carga en el punto, y que por tanto las cargas son las fuentes escalares de E. Si la densidad de carga es positiva tendremos un campo que emerge de ella (un manantial), mientras que si la densidad de carga es negativa tendremos un campo dirigido hacia ella (un sumidero):

.-La Ley de Ampere nos dice que el rotacional de B es la suma de una parte proporcional a la densidad superficial de corriente más otra proporcional a la variación temporal de E. Las cargas en movimiento generan magnetismo como veníamos dejando entrever y la variación de campo eléctrico, que no deja de ser otro efecto de movimiento de cargas, también contribuye a la creación del mismo. Precisamente debido a esto decimos que en ausencia de magnetismo (sin movimiento de cargas) estamos en el dominio de la electrostática (cargas quietas):

Visto esto, para llegar a la otra ecuación tensorial tenemos que definir primero el tensor dual de F. El dual de un tensor, aunque todavía no les he dedicado ninguna entrada, es otro tensor «ortogonal» al mismo que completa el espacio, y el ejemplo más claro lo tenemos con el producto vectorial en 3 dimensiones, donde el resultado es un vector perpendicular a los 2 originales, que junto a ellos crea una base para el espacio. Concretamente, el dual *F lo definiremos como:

, y en primer lugar uno ya puede observar que los campos eléctrico y magnético cambian de posición en el tensor. De hecho, es posible encontrar un sistema de referencia desde el que el tensor F se vea como su dual a través de una transformación de Lorentz como las que describimos en la relatividad especial.

Y con esto tenemos una de las conclusiones más relevantes del electromagnetismo: ¡el qué es E y qué es B depende del movimiento relativo entre el observador y el campo! ¡El campo magnético que ve un observador es un efecto relativista del campo eléctrico sobre otro observador con movimiento relativo! ¡Ambos campos son las dos caras del mismo ente, el campo electromagnético, que cuando no se propaga se muestra sólo en su versión eléctrostática!

Sin más rollo, la segunda ecuación tensorial, análoga a la primera, nos dice que el gradiente de *F es nulo:

, de donde se deducen las 2 ecuaciones homogéneas de Maxwell al hacer las operaciones pertinentes:

.-La Ley de la Divergencia Nula nos dice, en base a que experimentalmente no se ha visto lo contrario, que la divergencia de B es nula, y por tanto sus líneas de campo siempre van a ser curvas y cerradas. No existen fuentes escalares de B:

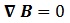.-La Ley de Faraday nos dice que el rotacional de E es una oposición a la variación de B con el tiempo. Cuando yo tengo un campo B y lo desplazo por el espacio, creo líneas cerradas y curvas de campo E que se le oponen. Faraday descubrió este efecto sobre bovinas conductoras, y dedujo la ley de inducción que hoy en día se usa en todos los circuitos, a saber, que al cambiar B creo corriente:

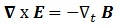Y finalmente, la combinación de estas 2 leyes (no demostrables) con las 2 anteriores nos dan las conocidas como las 4 ecuaciones de Maxwell que nos dicen todo lo que necesitamos saber sobre el campo electromagnético sin necesidad de nada más. En su versión tensorial, además, vemos que se reducen a 2 ecuaciones.

Por supuesto, de aquí no podemos deducir en ningún caso las fuerzas electromagnéticas de Coulomb y Lorentz, pero eso ya es dominio de la mecánica y no nos preocupan. Aquí simplemente nos interesa la naturaleza del campo, y no cómo actúa sobre las masas. En otra entrada será.

Lagrangiana y Ecuación de la Onda Electromagnética:

Para concluir esta entrada definiremos lo que se conoce como onda electromagnética, habitualmente conocida como luz cuando es visible. Podemos definirla empezando por presentar su lagrangiana asociada, y para ello necesitamos conocer algún escalar invariante del campo electromagnético. El principal candidato, evidentemente, es la contracción total de F consigo mismo:

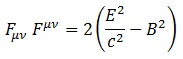, que es independiente del sistema de referencia y tiene unidades de Tesla cuadrado. Para que nos quede con unidades de energía, definimos la lagrangiana:

Y, si recordamos las ecuaciones de Euler-Lagrange:

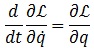, donde q era una coordenada espacial cualquiera y el punto indicaba derivada temporal, podemos convencernos fácilmente de que su análoga en el espacio-tiempo de Minkowski es:

, y aplicando esto a nuestra lagrangiana de onda electromagnética tenemos:

El primer miembro de la ecuación es evidente teniendo en cuenta la definición, y el segundo se ha anulado debido a que la lagrangina no depende de ninguna componente de A, sino de sus derivadas. Esta ecuación debería recordarnos a la primera ecuación tensorial de Maxwell, que habíamos relacionado con el cuadrivector de fuentes J, que sin embargo aquí ha desaparecido. La onda electromagnética se propaga sin fuentes, únicamente debido a la inducción mútua entre los campos E y B. Con esta condición extra, las 2 ecuaciones de Maxwell inhomogéneas pasan a ser también homogéneas:

Si a partir de aquí, calculamos el rotacional del rotacional de E teniendo en cuenta las propiedades del doble producto vectorial:

Tenemos esta ecuación diferencial, que por medio de la teoría de ondas sabemos que tiene como solución:

, es decir, una onda eléctrica propagándose según la dirección k a una velocidad c. Por supuesto, la onda electromagnética no siempre tiene que propagarse a esta velocidad, pero en eso profundizaremos en la siguiente entrada. Antes comprobemos para concluir que el campo B cumple la misma ecuación, y que por tanto ambos oscilan en fase:

Con esto termina la primera parte de estas dos entradas sobre el campo y las ondas electromagnéticas. En la siguiente veremos de qué factores depende la velocidad de propagación y qué es la radiación Cherenkov.