 Representación de Puntos en el Plano:
Representación de Puntos en el Plano:
Consideremos un plano donde dibujamos dos líneas perpendiculares que denominamos «OX» y «OY». Estas líneas se intersecan en un punto «O» que llamaremos el origen de coordenadas. El origen divide a los ejes en dos partes denominadas semiejes (semieje positivo y negativo). Cualquier punto del plano vendrá especificado por un par de números reales que denominaremos coordenadas del punto P = (px, py). Para obtener estas coordenadas trazamos una línea paralela al eje «Y» que pasa por «P»: el punto de corte de esta línea con el eje «X» se encuentra a una distancia «px» del origen. Análogamente, si trazamos una línea que pasa por «P» paralela al eje «X», la distancia del punto de corte con el eje «Y» al origen «O» es «py». A estas coordenadas se las denomina coordenadas cartesianas rectangulares.
A su vez, después de establecer los ejes coordenados podemos decir que el plano 2D está dividido en cuatro cuadrantes. En sentido contrario al avance de las agujas del reloj: I, II, III, IV. Los puntos que se encuentran en el eje «X» o eje de abscisas tienen coordenada «y = 0». Los puntos que se encuentran en el eje «Y» o de ordenadas tienen coordenada «x = 0». El origen de coordenadas será obviamente (0, 0).
En general denotaremos un punto en el plano mediante el par ordenado constituido por sus coordenadas (x, y). Abusando un poco del lenguaje podemos decir que que el plano donde se han introducido introducido las coordenadas cartesianas»x» e «y» es el plano «xy». Se cumple que dado un par arbitrario de números reales «x» e «y» existe siempre un punto «P» en el plano «xy» cuya abscisa es igual a «x» y cuya ordenada es igual a «y», que denotaremos por (x, y). Esta correspondencia es biunívoca. Definimos como los vectores unitarios coordenados i y j a aquéllos de longitud unidad orientados según los ejes coordenados.
Así pues:
, y por último:
Distancia entre dos puntos:
Sean dos puntos «P1» y «P2» en el plano «xy» de coordenadas (x1, y1) y (x2, y2), respectivamente. La distancia entre «P1» y «P2» en función de sus coordenadas es:
A esta distancia se le denomina también distancia euclídea en el plano, y cumple las siguientes propiedades:
- d(P1, P2) ≥ 0.
- Si d(P1, P2) = o, entonces P1 = P2.
- d(P1, P2) = d(P2, P1).
Consideremos el lugar geométrico de los puntos «r» que distan una distancia «r» de un punto «C» de coordenadas (x0, y0). Tenemos:
Esta es la ecuación canónica de una circunferencia de radio «r».
Coordenadas polares:
 Supongamos que tenemos definido en el plano l origen de coordenadas «O«, la unidad de escala de longitud y un eje «L» que pasa por el punto «O«. Sea «P» un punto arbitrario del plano que no coincide con «O«. Determinaremos su posición en el plano unívocamente mediante dos números:
Supongamos que tenemos definido en el plano l origen de coordenadas «O«, la unidad de escala de longitud y un eje «L» que pasa por el punto «O«. Sea «P» un punto arbitrario del plano que no coincide con «O«. Determinaremos su posición en el plano unívocamente mediante dos números:
- La distancia entre «P» y «O«, que denotaremos por «r».
- El ángulo «σ», medido en el sentido contrario al avance de las agujas del reloj, entre el semieje positivo «L» y la dirección «OM«.
Al par ordenado de valores (r, σ) se le denomina coordenadas polares del punto «P«. «r» es el radio polar y «σ» es el ángulo polar. Es habitual llamar a «O» el polo y a «L» el eje polar. Con la definición anterior, para todo punto «P» del plano, excepto el punto «O«, tenemos «r > 0» y «0 ≤ σ ≤ 2 π». Al polo «O» se le asigna «r = 0», mientras que el ángulo «σ» está indeterminado. Al sistema de coordenadas que acabamos de construir en el plano se le denomina sistema de coordenadas polares. Podemos relacionar el sistema de coordenadas cartesianas rectangulares con el de coordenadas polares:
- El polo «O» es el origen de coordenadas (0, 0).
- El eje orientado «X» es el eje polar. El eje «Y» forma un ángulo de «π / 2» respecto al eje «X». De este modo tenemos L = i.
Se llaman líneas coordenadas a aquéllas definidasmediante las condiciones la condición de que o bien «r» o bien «σ» sean constantes.
En coordenadas polares, estas líneas corresponden a circunferencias centradas en el origen y a semirrectas que pasan por el origen, respectivamente. Los vectores unitarios coordenados son vectores unitarios perpendiculares a las líneas coordenadas de cada punto, y con el mismo sentido del crecimiento de dicha coordenada. Con esta definición, los vectores «er» y «eφ» son ortonormales y su dirección depende del punto del espacio que consideremos:
La elección de un adecuado sistema de vectores unitarios tiene especial importancia en la expresión de los campos vectoriales. Interesa que las coordenadas curvilíneas elegidas se adecúen a la simetría que presente el campo. Consideremos por ejemplo una carga eléctrica «q» en el origen de coordenadas. El campo eléctrico generado tiene dirección radial y su módulo es:
, mientras que en coordenadas cartesianas (en 2D) tendríamos:
La relación entre coordenadas polares y cartesianas es:
A su vez, podemos escribir:
Ya vimos que la ecuación de la circunferencia de radio «r» centrada en el origen en coordenadas cartesianas es:
, mientras que en coordenadas polares es simplemente:
La ecuación, en coordenadas cartesianas, de una circunferencia centrada en un punto (x0, y0) arbitrario y radio «r» es:
Su expresion en coordenadas polares, siendo:
, se expresa del siguiente modo:
, y en caso de que la circunferencia pase por el eje de coordenadas (r0 = R), queda aún más simplificada:
Transformación de Coordenadas:
 En algunos casos puede resultar útil referir las coordenadas a sistemas de ejes a los originalmente planteados. Consideremos las siguientes transformaciones:
En algunos casos puede resultar útil referir las coordenadas a sistemas de ejes a los originalmente planteados. Consideremos las siguientes transformaciones:
- Traslaciones: tomamos un nuevo sistema de ejes coordenados cartesianos O’ X’ Y’ donde el origen de coordenadas O’ tiene coordenadas (x0, y0) referidas a los ejes coordenados O X Y. Obviamente se cumple que:
 A esta transformación se la denomina traslación.
A esta transformación se la denomina traslación. - Rotaciones: tomamos un nuevo sistema de ejes cartesianos O’ X’ Y’ en el que los ejes X’ e Y’ se giran solidariamente un cierto ángulo «α» en sentido antihorario.
Veamos cuál es la relación entre las coordenadas X Y referidas al sistema inicial y las coordenadas X’ Y’ referidas al sistema girado:
Dado un punto «P» en el plano de coordenadas (x, y), escribimos:
en el sistema de coordenadas sin transformar, mientras que en el transformado tenemos:
Sustituyendo con las anteriores igualdades:
Puesto que éstas son las componentes respecto a la base de vectores coordenados «i» y «j» deducimos:
Reflexión Especular:
Consideremos un sistema de coordenadas O X’ Y’ en el que se cumple que los ejes de abscisas coinciden (O X = O X’) y que el eje de coordenas transformado O Y’ tiene orientación opuesta al O Y. Para un punto «M» arbitrario la relación entre las coordenadas nuevas y las viejas será entonces:
Esto es una reflexión especular respecto al eje O X.
De modo análogo podemos hacer una reflexión especular respecto al eje O Y. Se puede demostrar que cualquier transformación de las coordenadas cartesianas rectangulares que conserve la distancia se puede descomponer en una traslación, giro y reflexión especular.
Curvas en el Plano:
Consideremos una curva en el plano X Y. La ecuación dada por:
se llama ecuación implícita de la curva. Los puntos del plano cuyas coordenadas (x, y) cumplen dicha ecuación se dice que son puntos de la curva. En esencia, la geometría analítica aborda el problema de las curvas en el plano desde las dos perspectivas:
- Encontrar la ecuación de una curva dadas sus propiedades geométricas.
- Encontrar las propiedades geométricas de una curva dada su ecuación.
Ecuaciones Paramétricas de una Curva:
Supongamos un punto «P» sobre una cierta curva y que para cada valor del parámetro «t» las coordenadas del punto son:
Estas son las llamadas ecuaciones paramétricas de la curva en función del parámetro «t». En el caso de una partícula que se mueva por el espacio físico que se mueva por el espacio describiendo la curva, este parámetro podría ser por ejemplo el tiempo.
Supongamos un círculo con centro en el origen y radio «R». Podemos escribir:
, con 0 ≤ σ ≤ 2 π. En este caso el parámetro de la curva es el ángulo «σ». A partir de las ecuaciones paramétricas podemos obtener la ecuación en forma implícita despejando el parámetro:
Consideremos las ecuaciones paramétricas siguientes:
Para eliminar el parámetro «σ» dividimos «x» por «a» e «y» por «b», de modo que:
Tenemos así la forma implícita de la ecuación de la curva, en este caso una elipse.
Conviene señalar que, en general, el conjunto de puntos que satisfacen las ecuaciones paramétricas no coincide con el conjunto de puntos que satisfacen la ecuación de la curva en su forma implícita. Consideremos el siguiente ejemplo:
Se cumple que:
, y por tanto la ecuación implícita de la curva es:
Se trata de una hipérbola. En esta ecuación el punto (-a, 0) es solución, pero no satisface las ecuaciones paramétricas originales.
Rectas en el Plano:
 Sea P un punto del plano R^2 y u un vector no nulo de R^2 (vector director). Se llama recta que pasa por P y tiene la dirección u al conjunto formado por los puntos r de R^2 tales que:
Sea P un punto del plano R^2 y u un vector no nulo de R^2 (vector director). Se llama recta que pasa por P y tiene la dirección u al conjunto formado por los puntos r de R^2 tales que:
, para cualquier valor de «λ».
Esta se denomina ecuación vectorial de la recta. Dos rectas definidas por:
serán la misma si y solo si los vectores «P1 – P2«, «u1» y «u2» son vectores proporcionales.
Si escribimos la ecuación vectorial usando coordenadas o componentes tendremos:
Éstas últimas se conocen como ecuaciones paramétricas de la recta en R^2.
Si despejamos «λ» obtendremos:
A ésta se la denomina ecuación continua o canónica de la recta.
Consideremos una línea recta que pasa por el punto P(Px, Py), y sea n = (nx, ny) un vector normal a la recta. Cualquier otro punto «r» que pertenece a la recta cumple que el vector «r – P» es perpendicular a «n«, y por lo tanto el producto escalar de ambos vectores debe ser nulo, surgiendo así la ecuación euclídea:
Sustituyendo llegamos inmediatamente a la ecuación normal:
Los coeficientes que acompañan a «x» e «y» tienen la interpretación de ser los coeficientes de un vector normal a la recta.
Posición Relativa a los Ejes Coordenados:
Supongamos una recta en el plano R^2 dada por la ecuación:
Tenemos:
- Si a = 0, entonces y = – c / b. Es una línea horizontal paralela al eje «X».
- Si b = 0, entonces x = – c / a. Es una línea vertical paralela al eje «Y».
- Si c = 0 entonces ax + by = 0. Es una línea que pasa por el origen de coordenadas.
Si en la ecuación general «b» no es nulo, entonces se puede escribir:
, o bien:
Dados dos puntos de la recta (x1,y1( y (x2,y2) podremos despejar «m» como:
, salvo tal vez un signo de reflexión especular.
Posición Relativa entre Dos Rectas:
Consideremos dos rectas en el plano dadas las ecuaciones:
Veamos si las rectas son paralelas o se cortan. Como ya sabemos, los coeficientes de «x» e «y» son las componentes de un vector perpendicular a la recta.
Por tanto el paralelismo entre dos rectas significa que los vectores (a1, b1) y (a2, b2) tienen la misma dirección, lo cual a su vez implica que los vectores (a1, b1) y (b2, – a2) son perpendiculares, con lo cual, por un producto escalar:
, de donde:
, y pendientes iguales implican paralelismo. La condición de paralelismo significa que no hay solución común a ambas ecuaciones.Si ademas obtenemos que:
, entonces las dos rectas son la misma, y aparecen infinitas soluciones.
Si por el contrario tenemos:
, entonces el sistema de ecuaciones tiene solución única y las rectas son secantes. Para que dos rectas sean perpendiculares sus vectores han de ser perpendiculares:
, o bien:
Ángulo entre Dos Rectas:
Consideremos dos rectas «r» y «s» del plano euclídeo dadas por las ecuaciones:
Los vectores normales a esas rectas son:
, respectivamente. El coseno del ángulo entre las dos rectas viene dado por el producto escalar:
, para 0 ≤ α ≤ 2 π.
Distancia de un Punto a una Recta:
Sea un punto P(xp, yp) del plano y una recta «r» dada por la acuación normal:
La distancia del punto «p» a la recta es la menor de las distancias de «p» a cualquiera de los puntos de la recta. Sea «r» el vector de posición de cualquier punto de la recta y «p» el vector de posición del punto (px, py), entonces la distancia «d» que buscamos es la proyección del vector «r – p» sobre la dirección perpendicular a la recta:
Curvas de segundo orden en el plano. Cónicas:
 Comenzaremos con una introducción particular a cada una de las tres cónicas. Posteriormente daremos una definición general de las cónicas y demostraremos sus propiedades.
Comenzaremos con una introducción particular a cada una de las tres cónicas. Posteriormente daremos una definición general de las cónicas y demostraremos sus propiedades.
Consideremos un punto «P» en el espacio tridimensional R^3, situado en la perpendicular al centro de una circunferencia en un plano «σ». Tracemos todas las rectas que pasan por «P» y algún punto de la circunferencia, así obtenemos un cono con vértice «P» y semiángulo «α».
.-Si intersecamos al cono con un plano perpendicular a su eje de simetría obtendremos una circunferencia.
.-Si intersecamos al cono con un plano inclinado que forma un ángulo mayor que «α» con su eje de simetría obtendremos una elipse.
.-Si lo intersecamos con un plano paralelo a una de sus generatrices obtendremos una parábola.
.-Si lo intersecamos con un plano que forma un ángulo menor que «α» con su eje de simetría obtendremos una hipérbola con dos ramas.
Hay muchos fenómenos naturales que conducen a secciones cónicas. La trayectoria de cuerpos en campos gravitatorios es un ejemplo. La trayectoria del extremo de una sombra de un palo sobre una superficie plana a lo largo de un día es también una sección cónica. Por ahora estudiaremos la elipse, la hipérbola y la parábola por separado.
La Elipse:
 Se llama elipse, que tiene por focos los puntos «F» y «F'» situados a distancia «2 c», y cuya constante es «2 a», siendo «a > c > 0, al lugar geométrico de los puntos «Pi» pertenecientes a R^2 tales que la suma de las distancias de «P» a los focos es la constante «2 a»:
Se llama elipse, que tiene por focos los puntos «F» y «F'» situados a distancia «2 c», y cuya constante es «2 a», siendo «a > c > 0, al lugar geométrico de los puntos «Pi» pertenecientes a R^2 tales que la suma de las distancias de «P» a los focos es la constante «2 a»:
Se llaman ejes de la elipse (por sus ejes de simetría) a la recta F F’ (eje focal o mayor) y a su mediatriz (eje secundario o menor). La intersección de los dos ejes de la elipse es el punto «O», centro de simetría. Los puntos de la elipse que se encuentran en sus ejes se llaman vértices (A y A’ en el eje mayor y B y B’ en el eje menor). Se verifica que:
Veamos ahora cuál es la ecuación de la elipse en coordenadas rectangulares suponiendo que su centro coincide con el origen de coordenadas y que sus ejes de simetria coinciden con los ejes de coordenadas. Tenemos:
La condición de la elipse será que la suma de las distancias de «P» a cada uno de los focos sean igual a «2 a»:
, que simplificado queda:
, que es la ecuación canónica o reducida de la elipse.
La elipse puede considerarse como una generalización de la circunferencia, pues si «a» = «b» la elipse se convierte en una circunferencia de radio «a».
Propiedades de la Elipse:
- La elipse de semiejes «a» y «b» está contenida en el rectángulo |x| < a, |y| < b. Es fácil demostrarlo ya que como
 , se tienen que cumplir:
, se tienen que cumplir:
- Los vértices de la elipse son:

- Los ejes «OX» y «Y» son ejes de simetría de la elipse. Si (x0, y0) es un punto de la elipse, entonces (- x0, y0), (x0, – y0) y (- x0, – y0) son también puntos de la elipse.
- Los puntos (c, 0) y (- c , 0) son los focos de la elipse, y «2 c» es la distancia focal. El parámetro
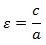 se denomina excentricidad de la elipse, y verifica 0 < e < 1 porque
se denomina excentricidad de la elipse, y verifica 0 < e < 1 porque Para una circunferencia tenemos
Para una circunferencia tenemos
Rectas Directrices y Redefinición de la Elipse:
Las rectas «δ1» y «δ2» dadas por:
se conocen como rectas directrices de la elipse (izquierda y derecha, respectivamente). Con su ayuda podemos definir la elipse como el lugar geométrico de los puntos del plano que verifican que la razón de la distancia a un foco y a la recta directriz correspondiente es igual a la excentricidad de la elipse:
La recta directriz derecha es:
La distancia de un punto «P» de la elipse a esta recta es:
, cumpliéndose «a > e x». La distancia de un punto de la elipse al foco derecho es:
Como (x, y) está en la elipse siempre que:
, se cumple:
Sustituyendo:
Vemos entonces que se obtiene:
Ecuaciones Paramétricas:
En la elipse se puede inscribir una circunferencia con centro (0, 0) y radio «r = b». A su vez, la elipse está inscrita en una circunferencia con centro en (0, 0) y radio «r = a».
La Hipérbola:
 Llamaremos hipérbola, que tiene por focos los puntos «F» y «F'» situados a una distancia «2 c», y cuya constante es «2 a», siendo 0 < a < c, al lugar geométrico de los puntos de R^2 tales que la diferencia de sus distancias a los focos es «2 a».
Llamaremos hipérbola, que tiene por focos los puntos «F» y «F'» situados a una distancia «2 c», y cuya constante es «2 a», siendo 0 < a < c, al lugar geométrico de los puntos de R^2 tales que la diferencia de sus distancias a los focos es «2 a».
Se llama eje focal o real a la recta «F F'», y eje secundario o imaginario a su mediatriz. Su punto de intersección, el origen «O», es el centro de simetría.
El eje «F F'» corta a la hipérbola en dos puntos «A» y «A'», que se llaman vértices, de modo que:
El eje imaginario no corta a la hipérbola, que tiene dos ramas, una a cada lado de este eje. A los puntos B(0, b) y B'(0, – b), con el parámetro «b» verificando la relación:
, se les conoce como extremos del eje imaginario.
Si se cumple que «a = b», entonces la hipérbola se dice equilátera.
Veamos ahora la ecuación de la hipérbola a partir de la relación dada. Sus focos son:
, por lo tanto tenemos, restando las distancias:
Elevando al cuadrado y operando obtenemos:
Propiedades:
- La hipérbola se haya fuera de la franja |x| < a. En efecto, basta ver que:
 , por lo tanto |x| ≥ a. Los puntos:
, por lo tanto |x| ≥ a. Los puntos: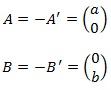 son los vértices de la hipérbola y los extremos del eje imaginario.
son los vértices de la hipérbola y los extremos del eje imaginario.
- Está contenida en la región comprendida entre las rectas:
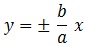 , que contiene el eje «OX». Para comprobarlo basta con tomar la desigualdad:
, que contiene el eje «OX». Para comprobarlo basta con tomar la desigualdad: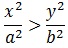 , con lo cual:
, con lo cual: Entonces:
Entonces: La hipérbola se halla contenida por tanto en dos regiones, una contiene la rama derecha y la otra a la izquierda. Estas rectas son, además, asíntotas de la hipérbola.
La hipérbola se halla contenida por tanto en dos regiones, una contiene la rama derecha y la otra a la izquierda. Estas rectas son, además, asíntotas de la hipérbola.
Otra Definición de la Hipérbola:
Denominamos de nuevo excentricidad de la hipérbola al parámetro:
Se cumple que e > 1. Las rectas:
se denominan rectas directrices de la hipérbola. Podemos definir entonces la hipérbola como el conjunto de puntos del plano para los que la razón entre la distancia al foco y a la recta directriz correspondiente es igual a la excentricidad. Igual que con la elipse:
Tomemos la recta:
Entonces:
, y por otra parte:
Por lo tanto vemos que se cumple la definición.
Ecuaciones Paramétricas:
Las ecuaciones paramétricas de una hipérbola de semiejes «a» y «b» son:
El doble signo da lugar a las dos ramas de la hipérbola.
Hipérbola Conjugada:
Dada la hipérbola de ecuación:
, se denomina hipérbola conjugada a aquella que tiene como ecuación:
Comparte las mismas asíntotas que la hipérbola original.
La Parábola:
 Llamamos parábola en el plano euclídeo, que tiene por foco el punto «F» y por directriz la recta «δ» situada a una distancia «p > 0» del foco «F», al lugar geométrico de los puntos que equidistan de «F» y «δ».
Llamamos parábola en el plano euclídeo, que tiene por foco el punto «F» y por directriz la recta «δ» situada a una distancia «p > 0» del foco «F», al lugar geométrico de los puntos que equidistan de «F» y «δ».
Llamamos eje de simetría de la parábola al eje perpendicular a la recta «δ» que pasa por el foco «F». El eje corta a la parábola en un punto «O», que se llama vértice. La parábola no tiene centro, y es una curva no acotada que carece de asíntotas.
Un punto pertenecerá a la parábola si verifica que:
Con lo cual:
La definición de la parábola por medio de su directriz es:
Dado que ambas distancias son iguales, la parábola es una cónica con excentricidad:
Foco, Directriz y Excentricidad:
Dados en el plano un foco «F», una recta directriz «δ» que no pasa por «F», y un número no negativo «e» llamado excentricidad, se verifica que el lugar geométrico de los puntos «P» tales que sus distancias a «F» y a «δ» se mantienen en relación constante e igual a «e» forman una cónica. Concretamente:
- Si ε < 1 obtenemos una elipse.
- Si ε = 1 obtenemos una parábola.
- Si ε > 1 obtenemos una hipérbola.
Cónicas Equivalentes:
Hasta el momento hemos estudiado las tres cónicas fundamentales a partir de sus ecuaciones reducidas. Estas ecuaciones son de segundo grado en coordenadas «x» e «y». Si cambiamos el origen de coordenadas o rotamos los ejes, las ecuaciones reducidas de las cónicas se transforman en general en ecuaciones de segundo grado, por lo que se les suelen expresar de un modo general como:
Obviamente, si multiplicamos esta ecuación por una constante «ρ», la nueva ecuación representa la misma cónica que la anterior, ya que ambas ecuaciones tienen el mismo conjunto de soluciones.
Categorías:Carrera, Matemáticas











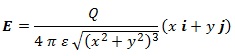








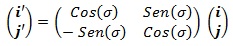

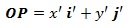

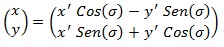









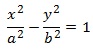




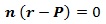

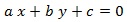














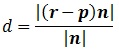

















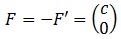



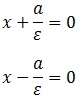

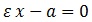





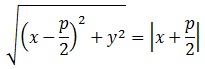



Hola, este espacio esta muy completo a mi punto de vista la verdad tiene muchas cosas de mi interés,pero me gustaria saber cuál es la interpretación de una inecuación analitica…no se si sería molestia el que me puedas explicar como se hace la interpretación.
Espero una respuesta.
Gracias.
A ver, tu pregunta me ha motivado para escribbir mas sobre esto
Veras, cuando tu escribes una ecuacion representas un conjunto de puntos de una dimension menos que la del espacio (rectas en el plano, planos en el espacio, superficies evolutivas en el espacio-tiempo), pero si en vez de eso escribes una inecuacion, tu restriccion de puntos no es tan grande
Supongamos que en el plano tienes la recta y = x. Es una gran restriccion de puntos. En cambio, si escribes y < x estas restringiendo los puntos que necesitas, pero menos, por lo que tienes toda la superficie bajo la recta. Es decir, con las inecuaciones, aumentas la dimension de la figura generada, pero solo hacia uno de los lados de tu recta/plano/superficie inicial
supongamos q en el plano tienes una recta y =x. es una gran restriccion de puntos . en cambio , si escribes y<x estas restringuiendo loa puntos q nesesitas
Me está gustando bastante este blog. Por cierto, en la parte del ángulo entre dos rectas es cos(α)=n1n2/|n1||n2|.
Gracias por avisar.