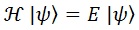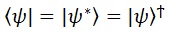En la entrada anterior introdujimos el campo de Schrödinger sin interacciones, viendo que se comportaba como una onda cuyo cuadrimomento p (energía y momento lineal) se correspondía con el vector de derivadas temporal y espaciales d, sin haber entrado a valorar mucho más del modelo. En esta entrada introduciremos el formalismo de Dirac, que no deja de ser otra forma de hablar de tensores y bases covariantes y contravariantes, cosas ambas ya vistas aquí, como paso previo para derivar de forma cómoda la incertidumbre de Heisenberg.

La base covariante o principal y la base contravariante:

El campo de Schrödinger ψ es un tensor de rango 0 (escalar) complejo, o si se quiere ver de otro modo, un vector con una componente real y otra compleja de módulo |ψ| y fase α:

En la base contravariante, por el contrario, tendremos su covector complejo conjugado:

La forma de definir el covector es tal que al multiplicarlo escalarmente por su vector el resultado sea 1.

Producto escalar extendido:

Cuando hacemos un producto escalar normalmente dos vectores A y B expresamos uno como covector y sumamos los productos de sus componentes:

Una función puede ser entendida como un vector de infinitas componentes, por lo que el producto escalar de dos funciones de x sería, análogamente:

El concepto de cofunción en general no se considera, por lo que ambas funciones se expresan con normalidad en la cuenta.

Por su parte, el campo de Schrödinger es un vector de 2 componentes y además una función, con lo que podemos definir con él un producto escalar que combine ambas propiedades:

Aquí x es el espacio. Como se puede observar, hemos impuesto que la integral del módulocuadrado del campo sea igual a 1 para poder decir que es una densidad de probabilidad. Que es positivo lo tenemos asegurado porque es el módulo de un número complejo, con lo que cumple los axiomas de Kolmogorov.

El formalismo de Dirac:

Como un concepto como el producto escalar, cuyo origen fue para la aplicación en vectores, es extendible a funciones y otros objetos siempre que cumpla unas condiciones ya comentadas, el objetivo de este formalismo es escribir conceptualmente sin centrarnos en la estructura concreta del objeto matemático con el que tratamos.

.-Estados:

De forma muy general, llamamos «estado» del sistema al objeto matemático que lo caracterice. En el caso que nos ocupa, al campo de Schrödinger libre, y lo escribimos del siguiente modo:

.-Operadores, autoestados y autovalores:

Podemos decir que un operador, por ejemplo A, es cualquier cosa actuando sobre nuestro estado si está puesta delante. En caso de que la actuación de un operador sobre el estado sea equivalente a algo proporcional al estado decimos que tenemos un autoestado de ese operador. Al factor de proporcionalidad, que podemos denominar a, le llamamos autovalor del autoestado:

¡Ojo! No todos los operadores tienen que tener autoestados, con lo que la segunda parte de la igualdad es un caso particular.

Un ejemplo de operador sería multiplicar por la coordenada x. Cuando multiplicamos por la coordenada x a nuestro estado simplemente hacemos eso, con lo que cualquier estado es autoestado de dicha coordenada con autovalor x:

Otro ejemplo de operador sería el número imaginario por el vector de derivadas. En la entrada anterior vimos que actuando sobre el campo de Schrödinger era equivalente al cuadrimomento p. Esto significa que el campo libre de Schrödinger es un autoestado de las derivadas de espacio y tiempo y que las componentes del cuadrimomento son sus autovalores:

En general, nos referiremos a lo que actúa a la izquierda como «operador momento», para distinguir del momento, que sería el resultado de aplicarlo al autoestado (parte derecha de la ecuación). En particular, cuando la derivada es la temporal hablamos del operador hamiltoniano H y el autoestado es la energía E:

.-Estados y operadores adjuntos:

Los coestados o estados adjuntos serían a los estados lo que los covectores son a los vectores: el objeto que necesitamos para definir el producto escalar. Los expresamos con los símbolos de forma opuesta a los estados y, en el caso de campos complejos, sabemos que son equivalentes a obtener el conjugado. A la operación de obtener el adjunto de un objeto la denotamos con el superíndice de una daga:

Podemos adjuntar varias cosas a la vez siendo respetuoso siempre con la regla fundamental, que es cambiar todo de orden siempre que lo que tengamos pueda no conmutar (matrices, derivadas…). En particular:

Aquí se puede observar que al conjugar el número imaginario aparece un signo menos, como comentamos. Esta regla, que puede parecer un poco rara al principio, es de vital importancia para que las cosas funcionen.

Una conclusión directa es que el autovalor adjunto debe ser el conjugado del autovalor:

.-Producto escalar:

Para representar el producto escalar entre coestado y estado simplemente los escribimos juntos, recordando que por definición este debe de ser igual a 1:

.-Media:

Teniendo todo este formalismo, podemos decir que la media del valor de un operador A es su integral entre coestado y estado, lo que representamos de los siguientes modos:

En particular, si A actúa sobre uno de sus autoestados, su valor medio es su autovalor:

Debido a las reglas vistas, la media del operador adjunto es el conjugado de la del operador:

Como más adelante necesitaremos recordarlo, es importante no perder de vista que las partes real e imaginaria de un número complejo se pueden obtener, usando el conjugado, de la siguiente forma:

Observables y operadores hermíticos o autoadjuntos:

Una propiedad experimental es que de un estado sólo podemos obtener información mediante sus autovalores reales, es decir, en los que no haya parte imaginaria. Yo puedo inventarme tantos operadores como quiera, pero si la función no es un autoestado suyo ese operador no será medible.

Decimos, consecuentemente, que un operador es un observable cuando su autovalor es real, cosa que equivale a decir que es igual a su adjunto:

Por lógica, decimos que un operador con estas características es autoadjunto, aunque es muy corriente referirse a ellos como hermíticos también.

Un ejemplo de cosa que podemos medir es la posición de nuestro campo, con lo que el operador posición debe ser hermítico:

Aquí x denota cualquier coordenada de tiempo o espacio.

Otro ejemplo un poco más chocante de observable es el cuadrimomento. Obviamente debe ser un observable porque involucra masa, energía y velocidad, pero hay un cambio de signo debido al número imaginario:

Aquí hemos expresado el operador momento adjunto y después lo hemos igualado al operador momento para que sea hermítico. Vemos que para que esto tenga sentido el vector de derivadas adjunto debe cumplir la relación:

Esto, no obstante, era de esperar puesto que ya vimos en la entrada anterior que la derivada del campo conjugado era opuesta a la del campo.

Por otra parte, siempre que tengamos un operador no hermítico podemos crear uno que sí lo sea multiplicándolo por su adjunto, lo que garantiza hermiticidad (recordando que tenemos que cambiar el orden al obtener un adjunto por si no conmutan):

Incertidumbre de las medidas:

Visto todo el formalismo de Dirac, podemos empezar a hacer cuentas interesantes.

.-Varianza, desviación típica y covarianza:

Supongamos ahora que tenemos un operador A cualquiera. Podemos definir su desviación con respecto a su valor medio del siguiente modo:

Este operador que hemos creado, por lógica, debe tener valor medio nulo, ya que la desviación media del valor medio ha de ser exactamente cero por la definición de media:

No obstante, la media de este operador elevado al cuadrado sí que puede ser distinta de cero, y es la varianza del sistema (no entro a filosofar sobre lo que es la varianza porque ya está en la entrada de estadística):

A su vez, definimos la desviación media como la raíz de la varianza:

Este valor nos indica cuánto se desplaza típicamente el valor medido más o menos del medio y es frecuente denominarlo también la incertidumbre estadística de la medida. Esta incertidumbre es de naturaleza intrínsecamente matemática y no de resolución.

Otro elemento útil es la covarianza entre dos operadores A y B:

Como es lógico, la covarianza de un operador consigo mismo es igual a su varianza.

.-Conmutador canónico:

Definimos el conmutador de los operadores A y B como el resultado de aplicar A B sobre el estado restando luego B A y lo representamos con corchetes. Si los operadores conmutan el conmutador es 0, como es lógico. En particular, denominamos conmutador canónico al de las componentes de tiempo y espacio con el de las componentes de energía y momento, que no es nulo:

En el último paso hemos reintroducido la métrica g, que en ausencia de campos gravitatorios toma la forma expuesta, donde las i denotan cualquier índice espacial. Con ella representamos la derivada de una coordenada respecto a otra. En resumen, el conmutador se expresa como:

.-El principio de incertidumbre de Heisenberg:

Consideremos las incertidumbres de dos operadores A y B. Multiplicándolos podemos encontrar la siguiente inecuación:

Yendo por pasos:

a) Usamos la definición de las incertidumbres.

b) Usamos que el producto de dos números cuadrados siempre es mayor o igual en módulo que el producto de dichos números al cuadrado. (Desigualdad de Cauchy-Schwartz)

c) Expresamos el módulo de un número complejo como la raíz de la suma de su parte real e imaginaria, ambas al cuadrado.

d) Usamos que lo anterior es obviamente mayor o igual que si consideramos sólo la parte imaginaria.

e) Expresamos la parte imaginaria como vimos más arriba.

f) La reescribimos en función del conmutador.

En resumen, el principio de incertidumbre nos dice que:

Como el producto debe tomar siempre un valor mínimo es imposible que la incertidumbre en ninguna de las dos medidas sea exactamente 0. En el caso particular de multiplicar las incertidumbres de una coordenada y su momento asociado tenemos:

Es importante recordar que estamos usando unidades naturales.

Aplicaciones del principio de incertidumbre:

.-Tiempo y energía:

En el caso de fijar componentes temporales tenemos la relación:

De aquí podemos deducir que como siempre existirá una incertidumbre mínima en la energía de un estado esa incertidumbre pone una cota a lo seguros que podemos estar de su principio de conservación. Si tomamos t como el tiempo más pequeño que dejamos que pase antes de medir de nuevo la energía de un sistema, podemos decir que esa es nuestra incertidumbre temporal y esto nos da más o menos (despreciando el factor 2) una resolución energética de la forma:

En particular, si medimos cada segundo las fluctuaciones en la energía serán extremadamente pequeñas, del orden del femtoeletrónvoltio:

Esta energía es más de un billón de veces inferior a la energía cinética de un electrón oscilando en torno a un núcleo, que ya estimamos de unos 13,6 eV. Consecuentemente, midiendo cada «tanto» tiempo podemos estar muy seguros de la conservación de la energía. No obstante, a medida que acortásemos el periodo de medición perderíamos resolución energética y la conservaría podría, y puede, no conservarse. La teoría cuántica de campos trabaja con interacciones dentro de intervalos de tiempo ridículamente pequeños durante los cuales la energía no es conservada.

.-Posición y momento:

De forma análoga, podemos imaginarnos un campo moviéndose dentro de una esfera de radio R dentro de la cual no podemos observar nada, como puede ser un electrón en un átomo o en un agujero negro. En ese caso, R fijaría nuestra incertidumbre espacial y la resolución en momento sería más o menos para un átomo de hidrógeno:

Sabiendo que el electrón en el átomo es no relativista, además, podemos obtener la resolución energética mediante la ecuación clásica para la energía cinética:

Y, ¡sorpresa! Obtenemos casi exactamente la energía del órbital básico del átomo de hidrógeno sin considerar en ningún momento que interacciona electromagnéticamente con el núcleo sólo usando su radio.

Podemos caracterizar más o menos de forma equivalente el sistema orbital de un electrón en torno a un núcleo diciendo que la energía asociada es debida a la incertidumbre estadística de no poder observarlo o debida a la interacción electromagnética.

En la próxima entrada analizaremos el campo de Schrödinger con interacción de forma general y en un caso particular sencillo.