Hace tiempo publiqué una entrada con la demostración de las reglas elementales de derivación, en la cual utilizamos la definición de derivada lo mínimo posible para justificarlas. Además, definimos el número e como aquel que hacía que la función f(x)=e^x fuese igual a su propia derivada.

No es ningún secreto, por otra parte, que los matemáticos suelen preferir demostrar las derivadas por definición y definiendo el número e con el siguiente límite:

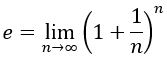
Así que en esta ocasión obtendremos las derivadas pertinentes empleando ambas reglas. No obstante, yo recomiendo para principiantes aprenderse las demostraciones que realicé en la otra entrada.

Definiciones alternativas del número e:

En esta ocasión nos interesará trabajar con su versión inversa. n tiende a infinito, pero cuando calculamos derivadas por definición nuestro límite tiene una h que tiende a 0, por lo que resulta más útil tener en mente:

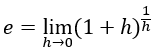
Otras expresiones alternativas que se fundamentan en lo mismo son:

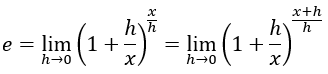
Siempre y cuando x sea un número diferente de 0.

Logaritmo natural:

Por definición, diremos que el logaritmo del número e es 1, es decir, trabajaremos en base natural:

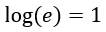
Y, teniendo en mente que el logaritmo de un número será el número al que hay que elevar e para que de como resultado dicho número, podemos razonar que:

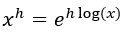
Límites relevantes:

Por último, antes de entrar en materia conviene justificar explícitamente algunos límites que aparecerán más adelante.

El primero surge cuando tenemos casi el número e, pero nos falta una x en el exponente. Para solucionar este problema, multiplicamos y dividimos el exponente por x, lo que nos lleva a:

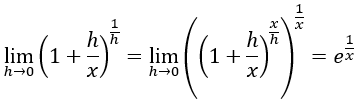
El segundo es similar, pero faltando h. Con el mismo razonamiento, podemos demostrar que:

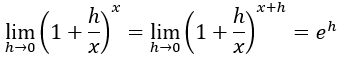
El tercero es un límite con un logaritmo dividido por un número que tiende a 0, al cual llamaremos w, y podemos introducirlo como un exponente dentro del logaritmo usando sus propiedades:

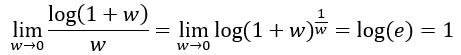
El cuarto es el mismo límite, pero cambiando numerador por denominador. Por cuestiones obvias el resultado también será 1:

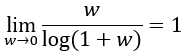
El quinto y último requerirá algo más de espacio para ser demostrado, y consiste en lo siguiente:

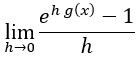
Para ver cómo simplificarlo, realizamos el siguiente cambio de variable por w:

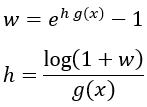
Teniendo en cuenta que cuando h tiende a 0 la variable w también se anula, siempre y cuando g(x) no sea infinito, podemos reescribir el límite del siguiente modo y, aplicando el límite anterior, calcularlo:

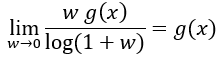
Y ya estamos listos para nuestro propósito en esta entrada.

Derivada del logaritmo:

Consideremos la función:

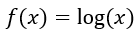
Su derivada será, aplicando al principio que la resta de dos logaritmos es igual a la división de sus argumentos y simplificando:

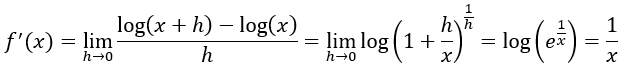
Derivada de la exponencial:

Si ahora consideramos la función:

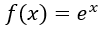
Su derivada será:

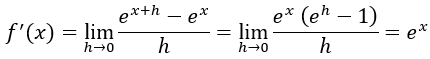
Derivada de x^x:

Por último, si tenemos la función:

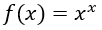
Su derivada será, teniendo en cuenta en el primer paso que podemos sacar del paréntesis x elevado a cada uno de los sumandos del exponente:

Y con esto concluimos. Espero que os sea de ayuda a los que os tengáis que pelear con demostraciones por definición.