En los comienzos de este blog muchas veces hablé de la teoría especial de la relatividad sin entrar en mucho detalle. Es entonces mi objetivo en esta entrada concluir con este tema de una vez, observándolo desde un punto de vista prácticamente matemático que no deje lagunas para no tener que volver sobre él.
Con la información de esta entrada posteriormente calcularemos la desviación de la órbita de mercurio, la variación de la longitud de onda de la luz al chocar con electrones, y algunos otros efectos interesantes.
Constancia de la Velocidad de la Luz:
Si recordamos los principios de la relatividad, se basaba únicamente en dos axiomas:
-La velocidad de la luz en el vacío es constante para cualquier observador.
-Las leyes de la física son equivalentes para todos los sistemas de referencia.
La constancia de la velocidad de la luz será, pues, nuestra base para deducir todas las ecuaciones posteriores. Recordemos que su valor es de:
 , pero para ahorrarnos el número la designaremos simplemente como «c».
, pero para ahorrarnos el número la designaremos simplemente como «c».
Supongamos que estamos ubicados en un espacio euclídeo de 4 dimensiones, donde la 4ª dimensión es el tiempo, en el sentido en el que lo analicé en esta entrada. Si desde el origen de coordenadas:
 lanzamos un rayo de luz, cumplirá que su distancia «espacial» al origen será:
lanzamos un rayo de luz, cumplirá que su distancia «espacial» al origen será:
 , ecuación que podemos asociar a una esfera evolutiva, como comenté en la entrada antes mencionada. Esta ecuación representa una esfera cuyo radio va aumentando con el tiempo. Si emitimos luz en el vacío, generamos una esfera de luz que va aumentando su radio a la velocidad de la luz.
, ecuación que podemos asociar a una esfera evolutiva, como comenté en la entrada antes mencionada. Esta ecuación representa una esfera cuyo radio va aumentando con el tiempo. Si emitimos luz en el vacío, generamos una esfera de luz que va aumentando su radio a la velocidad de la luz.
Podemos expresar esta ecuación en su forma implícita del siguiente modo:
 Ecuación que siempre será cierta para cualquier observador cuando hablemos de la luz que procede del origen.
Ecuación que siempre será cierta para cualquier observador cuando hablemos de la luz que procede del origen.
Cuadriposición:
Dado que tenemos las tres coordenadas espaciales de siempre y el tiempo como coordenada extra, y además para la luz se relacionan como está indicado arriba, es posible expresar el cuadrivector de posición de la luz con una coordenada «0» temporal y las coordenadas «1, 2 y 3» espaciales, expresadas como un vector de posición dentro del propio cuadrivector:
Como la ecuación que vimos antes para la luz es idéntica para todos los observadores, es una magnitud escalar relativista (no se transforma con los cambios de coordenadas), y por tanto tiene que proceder del producto escalar de dos cuadrivectores, en este caso cuadriposiciones. O dicho de otra forma, tenemos la garantía de que el producto escalar de la cuadriposición consigo misma para un haz de luz es nulo, y por tanto se tiene que definir como:
 Sabemos además, por la teoría de tensores recién vista, que todo producto escalar se puede expresar a través de una métrica:
Sabemos además, por la teoría de tensores recién vista, que todo producto escalar se puede expresar a través de una métrica:
 , y como en este caso la componente temporal se multiplica por sí misma normalmente, y a las otras les surge un signo «-«, tenemos que la nueva métrica, la métrica de Minkowski, deberá ser del siguiente modo:
, y como en este caso la componente temporal se multiplica por sí misma normalmente, y a las otras les surge un signo «-«, tenemos que la nueva métrica, la métrica de Minkowski, deberá ser del siguiente modo:
 Al hacer un producto escalar, las componentes espaciales aparecen con un signo negativo. Debido a ello, la métrica de Minkowski define los nuevos espacios de Minkowski de 4 dimensiones, con esta nueva versión de distancia y módulo.
Al hacer un producto escalar, las componentes espaciales aparecen con un signo negativo. Debido a ello, la métrica de Minkowski define los nuevos espacios de Minkowski de 4 dimensiones, con esta nueva versión de distancia y módulo.
Asimismo, si realizamos un producto escalar con un «-» delante, podemos usar esta métrica con el tiempo negativo y el espacio positivo, con la garantía de que el producto escalar también será un invariante.
Existen modos de evadir la métrica de Minkowski usando números complejos, como vimos en la entrada sobre cuaterniones. Podemos representar el mismo producto escalar del modo elemental si acompañamos a las componentes espaciales de los números hipercomplejos, o la métrica opuesta si hacemos sólo el tiempo complejo. Gracias a los complejos garantizamos que el producto escalar rudimentario (suma de componentes al cuadrado) hace que algunas tomen el signo negativo. No obstante, el uso de números complejos está mal visto desde dentro de la física teórica.
La cuestión es: ¿evade la métrica de Minkowski por completo la geometría compleja? La respuesta es «no». Recordemos que las componentes de la métrica se definían como el producto escalar de los vectores base del espacio, y si el producto escalar de 3 de ellos consigo mismos da «-1», y entre ellos es nulo, ¡estamos usando una base de vectores ortonormal compleja!
En resumen, en relatividad podemos trabajar con una base compleja y componentes reales (método de Minkowski), o con una base real y componentes complejas (método de cuaterniones). En esta entrada usaremos el método de Minkowski.
Líneas de Universo y Parámetro Natural:
Supongamos una partícula que no sea un haz de luz, es decir, que su velocidad no sea «c», moviéndose por el espacio de Minkowski según una determinada trayectoria. Como vimos en la teoría de curvas, es posible parametrizar todo el recorrido según un parámetro arbitrario. Escogeremos como norma siempre el tiempo del observador como elemento de parametrización de una trayectoria.
Como al parametrizar según el tiempo «t» del observador todas las componentes de la cuadriposición dependen exclusivamente de este, su producto escalar también lo hará. El producto escalar definirá la variación del parámetro natural «s» de la línea de universo, que después veremos que es idéntico a su longitud:
En el caso de un haz de luz, como ya hemos visto, el parámetro natural de su línea de universo es nulo, pero según las distintas velocidades puede ser también positivo y negativo.
Conos de Luz:
La variación del parámetro natural recién vista nos da una idea de la velocidad a la que se propaga la partícula en cuestión, de forma que:
- Si la variación es positiva se moverá más rápido en el tiempo que en el espacio (trayectoria tipo tiempo), lo que implica que el cuerpo se mueve más despacio que la velocidad de la luz.
- Si la variación es negativa se moverá más rápido en el espacio que en el tiempo (trayectoria tipo espacio), lo que implica que el cuerpo se mueve más rápido que la velocidad de la luz.
Dado que, hasta la fecha, no se sabe de nada que viaje más rápido que la velocidad de la luz, se considera que toda la materia sigue trayectorias tipo tiempo, y las trayectorias tipo espacio quedan relevadas a la ciencia ficción.
La velocidad que las separa, la velocidad de la luz, define una gran barrera para la física, mientras que vuelve interesante la acción-consecuencia, pues un suceso en un punto de dimensiones espaciales «A» no podrá tener ninguna consecuencia sobre otro punto de dimensiones espaciales «B» hasta que la luz haya recorrido la distancia entre ellos.
El ejemplo más clásico de esto son el Sol y La Tierra. La luz solar tarda 8 minutos en llegar hasta nosotros, por lo que si el Sol se apagase, tardaríamos 8 minutos en enterarnos.
Un suceso de coordenadas «A» sólo puede estar relacionado causalmente con un suceso de coordenadas «B» si el producto escalar de Minkowski consigo mismo del cuadrivector que los une es positivo, pues de lo contrario la información tendría que viajar más rápido que la luz.
Geométricamente, desde un suceso «A» se emite una «señal luminosa de causación» que se propaga como una esfera a la velocidad de la luz. Los puntos del espacio-tiempo que vayan quedando dentro de dicha esfera pueden estar relacionados causalmente con «A», y el resto no. Asimismo, «A» sólo puede ser consecuencia de sucesos «B» que lo contengan en su señal de causación.
Como la esfera de causación antes definida:
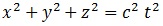 vive en 4 dimensiones, y éstas acostumbran a ser difíciles de representar gráficamente, en general se omite una coordenada (pongamos «z») y se representa en 3 dimensiones:
vive en 4 dimensiones, y éstas acostumbran a ser difíciles de representar gráficamente, en general se omite una coordenada (pongamos «z») y se representa en 3 dimensiones:
 Debido a esta aproximación, si representamos la esfera de luz en el espacio tridimensional, siendo la coordenada vertical el tiempo, obtenemos un cono de eje vertical centrado en el origen y de ángulo con la vertical (visto en teoría de superficies) igual a:
Debido a esta aproximación, si representamos la esfera de luz en el espacio tridimensional, siendo la coordenada vertical el tiempo, obtenemos un cono de eje vertical centrado en el origen y de ángulo con la vertical (visto en teoría de superficies) igual a:
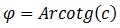 , que debido a que la velocidad de la luz es muy grande, se puede aproximar a 90º en un entorno próximo al origen. De hecho, el retraso de la señal de causación entre dos puntos opuestos en la tierra es inferior a la millonésima de segundo, e internet es el mejor ejemplo de ello.
, que debido a que la velocidad de la luz es muy grande, se puede aproximar a 90º en un entorno próximo al origen. De hecho, el retraso de la señal de causación entre dos puntos opuestos en la tierra es inferior a la millonésima de segundo, e internet es el mejor ejemplo de ello.
En resumen, el cono de luz, es una aproximación geométrica a la esfera de luz , y representa la barrera causal entre varios sucesos.
Rotaciones Espacio-Temporales:
Cuando vimos la geometría plana, podíamos girar los ejes de la base distintos ángulos para ver las coordenadas espaciales desde otra perspectiva. Asimismo, en el espacio, podíamos rotar los ejes con los ángulos de Euler.
En el espacio-tiempo, un cambio de observador supone rotar el eje temporal con el eje espacial de la dirección del movimiento según las distintas velocidades, de modo que si un observador ve a otro moverse a una velocidad «v», el concepto de tiempo y distancia que tendrán ambos será muy distinto. Para ver cualitativamente esta variación, será necesario introducir un nuevo concepto:
Transformaciones de Lorentz:
Supongamos una vez más una esfera de luz que parte del origen de coordenadas. Un observador en el origen podrá apreciar la ecuación:
 para la posición del haz de luz. En cambio, otro observador que se aleje también del origen con velocidad «v» verá una ecuación distinta:
para la posición del haz de luz. En cambio, otro observador que se aleje también del origen con velocidad «v» verá una ecuación distinta:
 Esto debe ser así porque recordemos que era una ecuación invariante frente a cambios de coordenadas. Si tenemos en cuenta las condiciones que hemos supuesto, las coordenadas y e y’ serán iguales, así como z y z’, por lo que hay que demostrar que las variaciones en «x» y en «t» se compensan, y además, por la forma de la ecuación, si el tiempo relativo al segundo observador es mayor, la distancia por la luz que observa también tendrá que ser mayor, y viceversa.
Esto debe ser así porque recordemos que era una ecuación invariante frente a cambios de coordenadas. Si tenemos en cuenta las condiciones que hemos supuesto, las coordenadas y e y’ serán iguales, así como z y z’, por lo que hay que demostrar que las variaciones en «x» y en «t» se compensan, y además, por la forma de la ecuación, si el tiempo relativo al segundo observador es mayor, la distancia por la luz que observa también tendrá que ser mayor, y viceversa.
La hipótesis de Lorentz consiste en suponer que nos encontramos ante una transformación lineal básica:
Esta será, pues, la matriz de transformación de Lorentz. Como hemos razonado antes que las alteraciones en tiempo y espacio deben proceder de rotaciones del eje temporal y espacial, el determinante de la matriz de Lorentz, que es una matriz de giro, debe ser unitario:
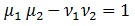 Esto volverá a ser relevante al final.
Esto volverá a ser relevante al final.
Sustituyamos estas transformaciones lineales en la ecuación del observador en movimiento:
Si desarrollamos los cuadrados y reorganizamos un poco:
 Las dos primeras ecuaciones representan hipérbolas en el plano, y como vimos en teoría de curvas las podemos parametrizar según la geometría hiperbólica, pues los senos y cosenos hipérbolicos son las únicas funciones que cumplen que su diferencia de cuadrados sea siempre 1:
Las dos primeras ecuaciones representan hipérbolas en el plano, y como vimos en teoría de curvas las podemos parametrizar según la geometría hiperbólica, pues los senos y cosenos hipérbolicos son las únicas funciones que cumplen que su diferencia de cuadrados sea siempre 1:
, donde los senos tienen una ambigüedad de signo, por ahora indeterminado. Si vamos con esto a la última ecuación que obtuvimos:
, que sólo se cumplen si ambos ángulos son iguales:
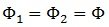 Así pues, la transformación de Lorentz queda parametrizada como:
Así pues, la transformación de Lorentz queda parametrizada como:
, que tal y como exigíamos, posee un determinante unitario: es una rotación del eje temporal con un eje espacial. Es importante observar que mientras que los ejes espaciales se rotan con ángulos elípticos, el eje temporal se rota con ángulos hiperbólicos debido a la geometría de Minkowski.
Ahora bien, tenemos la transformación de Lorentz expresada en función de un ángulo hiperbólico que desconocemos, y que obviamente deberá depender de la velocidad «v» del observador en movimiento. Si queremos expresar «Φ» según «v» con convencimiento será conveniente seguir trabajando con los cuadrivectores.
Cuadrivelocidad:
Supongamos que queremos obtener la velocidad de una partícula respecto a un observador dado. Podemos derivar su cuadriposición respecto al tiempo del observador:
, sin embargo, como el tiempo del observador depende de la velocidad, esta cuadrivelocidad depende del sistema de coordenadas, y por tanto no es un vector. Si queremos que sea un vector, debemos derivarla respecto a algo que sea igual en todos los sistemas de coordenadas.
Si recordamos la teoría de curvas, la longitud de la curva era idéntica para todas las parametrizaciones (en este caso todos los observadores), y en este caso la longitud de la curva será, según el tiempo del observador:

 Como ya vaticinamos, el parámetro natural es la longitud de la línea de universo, y cumple anularse cuando la velocidad de la partícula es «c», ser positivo si la velocidad es inferior a la de la luz, y ser negativo si la velocidad es superior a la de la luz.
Como ya vaticinamos, el parámetro natural es la longitud de la línea de universo, y cumple anularse cuando la velocidad de la partícula es «c», ser positivo si la velocidad es inferior a la de la luz, y ser negativo si la velocidad es superior a la de la luz.
El parámetro propio, como ya vimos y acabamos de volver a demostrar, es un escalar, pero es un escalar con unidades de longitud, y si derivamos respecto a él no obtendremos una velocidad sino algo carente de unidades. Necesitamos un escalar con unidades de tiempo.
Tiempo Propio:
Una propiedad muy importante de la teoría especial de la relatividad es que como la velocidad de la luz es constante, cualesquiera dos magnitudes que se relacionen a través de la velocidad pueden ser equivalentes.
Esto, para empezar, quiere decir que las longitudes las podemos convertir en tiempos dividiéndolas por «c» y viceversa, de modo que el tiempo propio de una partícula lo podemos definir como:
 , con la garantía de que también será un escalar. Expresar el tiempo según el espacio no es ninguna locura ni viceversa. Esta ecuación que acabamos de ver es la forma matemática de hablar de años luz, minutos luz, segundos luz y demás distancias que dependen del tiempo.
, con la garantía de que también será un escalar. Expresar el tiempo según el espacio no es ninguna locura ni viceversa. Esta ecuación que acabamos de ver es la forma matemática de hablar de años luz, minutos luz, segundos luz y demás distancias que dependen del tiempo.
Ahora bien, si calculamos el tiempo propio en función del del observador externo obtenemos:
 Esta expresión tiene más utilidad expresada como una derivada:
Esta expresión tiene más utilidad expresada como una derivada:
 , y para simplificar, denominamos «γ» al segundo miembro de la ecuación:
, y para simplificar, denominamos «γ» al segundo miembro de la ecuación:
 En el hipotético caso de que la velocidad sea constante, «γ» también lo será, y obtendremos que el tiempo que mide el observador externo es igual o mayor que el tiempo propio del objeto:
En el hipotético caso de que la velocidad sea constante, «γ» también lo será, y obtendremos que el tiempo que mide el observador externo es igual o mayor que el tiempo propio del objeto:
Factor Gamma:
El factor «γ» es muy interesante de analizar, pues si la velocidad del observador externo es 0 vale 1, y por tanto ambos tiempos son iguales, pero si la velocidad del observador externo se aproxima a «c» el tiempo «t» es infinitamente mayor que el tiempo propio.
El tiempo de un observador externo siempre es mayor que el propio, y por tanto la forma de medir el menor tiempo posible para un suceso es moverse con él (velocidad relativa 0). Paradójicamente, si dos personas se desplazan a una velocidad «v» entre ellas, cada una medirá un tiempo dilatando de la otra según «γ», mientras que sus tiempros propios serán iguales.
Ahora que poseemos el tiempo propio al fin podremos obtener la verdadera cuadrivelocidad:
 La cuadrivelocidad es la cuadrivelocidad relativa incrementada en el factor «γ», igual que el tiempo relativo es el tiempo propio multiplicado por «γ».
La cuadrivelocidad es la cuadrivelocidad relativa incrementada en el factor «γ», igual que el tiempo relativo es el tiempo propio multiplicado por «γ».
Habiendo visto ya que el tiempo se transforma con el factor «γ», podemos volver a las transformaciones de Lorentz. Supongamos una partícula quieta con tiempo propio «τ», que observamos desde fuera con una velocidad «v». La transformada de Lorentz sería:
 Ya tenemos el ángulo hiperbólico en función de la velocidad relativa. Si ahora queremos el seno hiperbólico, deberemos obtenerlo de la relación:
Ya tenemos el ángulo hiperbólico en función de la velocidad relativa. Si ahora queremos el seno hiperbólico, deberemos obtenerlo de la relación:
 , con lo que la transformación de Lorentz nos resulta:
, con lo que la transformación de Lorentz nos resulta:
 , donde definitivamente nos hemos quedado con el signo negativo bajo el argumento de que si el observador se mueve con una determinada velocidad, verá al otro cuerpo irse en la dirección contraria por efectos relativistas.
, donde definitivamente nos hemos quedado con el signo negativo bajo el argumento de que si el observador se mueve con una determinada velocidad, verá al otro cuerpo irse en la dirección contraria por efectos relativistas.
Suma de velocidades:
Si queremos saber qué velocidad medirá el nuevo observador de la transformación de Lorentz para el otro cuerpo, teniendo en cuenta la velocidad medida original «u» y la relativa entre ambos «v», lo lógico podría ser pensar en una suma, pero si dividimos el espacio recorrido por la partícula en el nuevo sistema entre el tiempo en el nuevo sistema obtenemos algo bien diferente. Supongamos, para que haya adicción de velocidades, que el observador 2 viaja en dirección opuesta a la partícula observada (signo negativo):
La suma de dos velocidades en relatividad no es la suma directa, sino que en el divisor aparece un término relativista destinado a asegurarse de que la velocidad nunca supere la de la luz. Veamos que si una de las dos velocidades es «c», v’ se convierte automáticamente en «c»:
 Rapidez o Velocidad Hiperbólica:
Rapidez o Velocidad Hiperbólica:
Ya que hemos calculado la relación entre el ángulo hiperbólico y la velocidad relativa, es interesante buscarle un sentido físico a dicho ángulo. Para ello, obtengamos su tangente hiperbólica:
 «Φ» es una magnitud que oscila entre «-∞» e «∞», mientras que el cociente entre «v» y «c» sólo puede tomar valores entre «-1» y «1», igual que la tangente hiperbólica. Es por eso que decimos que «Φ» representa una velocidad sin límites, hiperbólica, que nosotros observamos reducida a la escala [-1, 1] por efectos relativistas.
«Φ» es una magnitud que oscila entre «-∞» e «∞», mientras que el cociente entre «v» y «c» sólo puede tomar valores entre «-1» y «1», igual que la tangente hiperbólica. Es por eso que decimos que «Φ» representa una velocidad sin límites, hiperbólica, que nosotros observamos reducida a la escala [-1, 1] por efectos relativistas.
«Φ», la rapidez, representa la «verdadera velocidad» de los cuerpos, la que puede llegar hasta el infinito, mientras que «v» es un límite de nuestra percepción que no puede apreciar velocidades más altas. En base a esto, la velocidad hiperbólica de la luz es infinita, pero nosotros, limitados, sólo podemos medir los 300 000 km/s habituales.
En límites en los que «Φ» sea muy pequeño, la tangente hiperbólica vale «Φ», y encontramos una relación más cercana entre ella y «v», pero a medida que crece la diferencia se va haciendo más notoria.
Teniendo en cuenta esto, «Φ» es una magnitud mucho más atractiva que «v», puesto que representa la velocidad infinita que siempre creimos posible hasta la llegada de la relatividad. Debido a que «Φ» no tiene límites, la anterior fórmula de adicción de velocidades no es necesaria, y la composición de velocidades hiperbólicas es igual a la suma de las mismas sin ningún término relativista.
Sobre este tema volveré en algún momento más adelante, así que no voy a realizar ninguna cuenta en esta entrada.
Unidades Naturales:
Volvamos ahora a la cuadrivelocidad:
 El cuadrado de su módulo se definiría como:
El cuadrado de su módulo se definiría como:
 , que es una expresión bastante fea. En cambio, si escogemos el sistema de unidades en el que «c» vale «1», y por tanto «v» sólo tomaría valores entre «0» y «1», la expresión toma otro tono, pues:
, que es una expresión bastante fea. En cambio, si escogemos el sistema de unidades en el que «c» vale «1», y por tanto «v» sólo tomaría valores entre «0» y «1», la expresión toma otro tono, pues:
 decimos que igualar «c» a la unidad es usar el sistema natural de unidades, pues, debido a que simplifica mucho todas las ecuaciones relativistas, empezando por esta.
decimos que igualar «c» a la unidad es usar el sistema natural de unidades, pues, debido a que simplifica mucho todas las ecuaciones relativistas, empezando por esta.
Cuadrimomento:
Podemos obtener el cuadrimomento relativista del mismo modo que el momento lineal clásico, multiplicando la cuadrivelocidad por la masa del cuerpo en movimiento:
 Para simplificar la expresión, definimos el momento relativista como:
Para simplificar la expresión, definimos el momento relativista como:
En unidades naturales:
 Dado que el módulo del cuadrivector «V» era «1» en unidades naturales, y ahora sólo lo hemos multiplicado por la masa, el cuadrado del módulo del cuadrimomento en unidades naturales será:
Dado que el módulo del cuadrivector «V» era «1» en unidades naturales, y ahora sólo lo hemos multiplicado por la masa, el cuadrado del módulo del cuadrimomento en unidades naturales será:
Si volvemos atrás un momento, recordaremos que cualquier para de magnitudes que se puedan relacionar a través de la velocidad son equivalentes en relatividad.
En base a ello definiremos la energía relativista como la masa multiplicada dos veces por la velocidad de la luz, y además incrementada en un factor «γ»:
 , que en el caso de que la velocidad sea nula es equivalente a:
, que en el caso de que la velocidad sea nula es equivalente a:
 Para introducir esto en el cuadrimomento, advertimos que:
Para introducir esto en el cuadrimomento, advertimos que:
 En unidades naturales obtendremos:
En unidades naturales obtendremos:
 Si calculamos el cuadrado de su módulo llegamos a la expresión de la energía relativista en unidades naturales, recordando que ya calculamos antes el cuadradado del módulo del momento y que era constante:
Si calculamos el cuadrado de su módulo llegamos a la expresión de la energía relativista en unidades naturales, recordando que ya calculamos antes el cuadradado del módulo del momento y que era constante:

 Toda partícula, quieta o en movimiento, tiene asociada una energía debida a su masa: la masa es energía condensada. Además, a medida que la masa se acelera, genera más energía. Recordando cómo definimos la energía, obtenemos:
Toda partícula, quieta o en movimiento, tiene asociada una energía debida a su masa: la masa es energía condensada. Además, a medida que la masa se acelera, genera más energía. Recordando cómo definimos la energía, obtenemos:
 Asimismo, si consideramos que la energía cinética «T» es la debida a la velocidad:
Asimismo, si consideramos que la energía cinética «T» es la debida a la velocidad:
 , de donde obtenemos la expresión para la energía cinética relativista:
, de donde obtenemos la expresión para la energía cinética relativista:
 Si la desarrollamos en serie de Taylor, obtenemos que para velocidades muy pequeñas la energía cinética es:
Si la desarrollamos en serie de Taylor, obtenemos que para velocidades muy pequeñas la energía cinética es:
Categorías:Carrera, Física, Relatividad









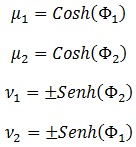

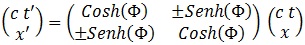






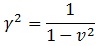



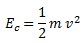
¿Cómo se puede creer en un absurdo tan grande como el segundo postulado de la relatividad einsteiniana? ¿porque es lo que se lleva ahora? Pobres de nosotros.
Porque funciona, y gracias a él tienes GPS que te pueden orientar, además de explicar cosas como por qué las partículas que llegan del espacio viven más tiempo que sus gemelas terrestres (se mueven más rápido).
El GPS es que dice que no funciona. Lo dice Ronald Hatch, que es la máxima autoridad en GPS. Y el físico Bryan Wallace en ‘The farce of physics’. Las partículas a las que te refieres viven más porque están sufriendo aceleración (negativa) mientras entran en la atmósfera, no por su velocidad. Entiendo que tú consideres verdad a lo que dice la física oficial, aún no te has percatado de que son todas mentiras
Hola, José Miguel,
Me aburrís de sobremanera los que habláis de la «física oficial» y la «no oficial», así que te voy a contestar una vez. A la próxima te anulo el comentario de forma acorde a mis criterios de moderación que puedes leer por arriba.
Las partículas necesitan estar siendo sometidas, efectivamente, a una variación de campo gravitatorio para que la dilatación temporal salga, pero la forma de calcular cuánto aumenta su vida la facilita la relatividad especial, salvo que te metas en cuerpos muy masivos como una enana blanca, una estrella de neutrones o un agujero negro. En casos sencillos como la Tierra, la relatividad general dice el tiempo de quién se dilata y la especial cómo calcularlo.
Dicho esto, reitero que no te voy a pasar un comentario más. Ya me he pasado por tu blog y eres un magufazo de élite.
Gracias por tu magnífico blog, Adrián. Trato de entender por qué la métrica de Minkowski es la adecuada para expresar las distancias en la mecánica relativista, y en todas partes me encuentro conque simplemente se da casi como axioma, sin derivarla ni dar explicaciones. En tu artículo, en la sección «Métrica de Minkowski», acabas llegando a ella, pero desgraciadamente sigo sin entenderlo. No entiendo por qué «tenemos la garantía de que el producto escalar de la cuadriposición consigo misma para un haz de luz es nulo, y por tanto se tiene que definir como:…»
Sería válido para un haz de luz, y RR = 0, pero no tiene por qué serlo para un evento donde sólo varíe la coordenada temporal, por ejemplo. Aunque probablemente yo esté equivocado, y es porque no lo acabo de entender bien.
Quizá lo tengas explicado en otro artículo de tu blog. Si es así, estaré encantado de leerlo allí.
Disculpa esta disquisición quizá algo simple, y gracias nuevamente.
Hola, Jose Luis, tienes toda la razón en tu comentario. Se da como axioma acorde con lo que pasa con la luz y se ve que funciona y predice montones de cosas útiles (retrasos de satélites, gravedad, teorías cuánticas de campos y cuerdas…). No obstante te diré que hay varias teorías que plantean otros axiomas (de las que aún no he hablado) como la relatividad especial de escala, de la que podrás encontrar poca información por internet porque es reciente. Igual en inglés, doubly special relativity, ya hay algo más que cuando la tuve que mirar yo. Básicamente introducen la longitud de Planck como otro invariante relativista.
Hola Adrián,
Muy interesante esta entrada sobre Relatividad Especial con explicaciones muy aclaradoras. En el caso de la Energía Relativista, una sugerencia para clarificar por qué se define así sería mostrar cómo se obtiene la energía cinética relativista como resultado del trabajo de una fuerza que acelera el cuerpo desde el reposo hasta una velocidad v. El resultado muestra que dicha energía cinética es la diferencia entre la energía total menos la energía en reposo.
También quería aprovechar para sugerir una entrada en tu blog sobre la Relatividad Especial de Escala. He leído algo sobre ella en el libro Las Dudas de la Física del Siglo XXI de Lee Smolin. Profundiza la Relatividad de Einstein permitiendo que la velocidad de los fotones varíe según la frecuencia (siendo la misma para todos los observadores a cada frecuencia supongo) consiguiendo con ello que todos los observadores coincidan en el valor de la longitud de Planck y en que esta es la mínima posible.
Un saludo,
Fran
Hola, gracias por pasarte. Tomo nota de la petición.