En la última entrada sobre cuerdas vimos que al cuantizarlas sucedía algo muy problemático: el operador fundamental de Virasoro, relacionado con las vibraciones, producía un factor d en principio infinito que no tendría que estar ahí. Para evitar dicho inconveniente, o bien la suma de todos los números naturales no era infinita o bien el número de dimensiones espaciales no era tres. En esta entrada veremos que en realidad tendrían que suceder ambas cosas para que el modelo fuese 100% consistente, concluyendo que el número de dimensiones espaciales adecuado es 25, que junto con el tiempo darían 26 dimensiones en total.
Antes de ponerme a redactar esta entrada he pensado largo y tendido sobre el mejor modo de explicar de forma intuitiva por qué la corrección de una teoría puede depender del número de dimensiones, pero lo cierto es que me he visto incapaz. Afortunadamente, no soy el único. Leonard Susskind, uno de los fundadores de la teoría de cuerdas dice en su libro «El paisaje cósmico» lo siguiente:
«Como profesor de física, odio contar a los estudiantes algo importante y luego decirles que no puedo explicarlo. Que es demasiado avanzado. O que es demasiado técnico. Paso mucho tiempo imaginando la forma de explicar cosas difíciles en términos elementales. Una de mis mayores frustraciones es que nunca he conseguido encontrar una explicación elemental de por qué la teoría de cuerdas es acertada solo si el número de dimensiones es de diez. Ni lo ha conseguido nadie.»
Leonard Susskind
Lo cierto es que comprender esto requeriría tener interiorizada de una forma por ahora sobrehumana la mecánica cuántica y, en particular, los conmutadores cuánticos. Todos los físicos tenemos claro haciendo las cuentas que en mecánica cuántica no es posible medir simultáneamente la posición y momento de una partícula porque no conmutan, y que lo mismo sucede con el tiempo y la energía, así como con los giros respecto a diferentes ejes. Sin embargo, qué es cualitativamente el resultado de un conmutador resulta poco o nada intuitivo. Teniendo su valor es «fácil» calcular todo, pero no lo es en absoluto interpretar dicho valor.
¿Por qué, cualitativamente, el conmutador de posición y momento da como resultado un número complejo multiplicando a la geometría/métrica del espacio? Cuando a una persona esta le resulte una cuestión trivial en términos de «vacas esféricas» (analogías sencillas) estaremos más cerca de explicar de forma sencilla por qué la teoría de cuerdas requiere de múltiples dimensiones.
Magnitudes conservadas en teoría de cuerdas:
Hasta ahora estábamos trabajando con cuerdas relativistas abiertas y cerradas. Su estado de vibración podía variar según la posición σ sobre la cuerda y según el tiempo τ transcurrido. En las cuerdas abiertas imponíamos, no obstante, que las derivadas respecto a σ en sus extremos fuesen nulas. Ambas cumplían la ecuación diferencial de una onda: sus derivadas segundas temporales eran iguales a sus derivadas segundas naturales:
Inciso: en esta entrada las ecuaciones me han quedado más pequeñas por motivos que resultarán evidentes. Podéis hacer clic para ver con más detalle.
Dada una cuerda, podíamos definir su cuadrimomento p del siguiente modo según la tensión T de la cuerda:
Recordemos que s valía 1 para cuerdas abiertas y 2 para cuerdas cerradas.
Análogamente, podemos definir también el cuadritensor M del siguiente modo:
Es trivial verificar que el cuadrimomento se conserva frente a variaciones temporales aplicando la ecuación de onda:
El último término se anula en las cuerdas abiertas por haber impuesto que las derivadas naturales en los extremos serían nulas y en las cerradas porque el punto inicial y el punto final coinciden. Lo mismo es aplicable para demostrar la conservación de M:
Nótese que en la cuarta igualdad se hace lo mismo que en la segunda, pero al revés y con σ.
Debido a su conservación, estas magnitudes son particularmente relevantes en el análisis de cuerdas relativistas, y la segunda será la fuente de todos nuestros males.
Conmutadores de M:
Recordemos el conmutador elemental entre la posición de la cuerda y su derivada temporal, que en términos de la métrica de Minkowski η y la función delta de Dirac era:
Las flechas hacían referencia al valor de sigma del término de la izquierda y al de la derecha dentro del conmutador.
Usando esto con mucha paciencia y teniendo en cuenta las reglas de operaciones con conmutadores podemos calcular el conmutador genérico entre dos cantidades M:
Y al combinar este resultado con coordenadas cono luz, resulta que el conmutador de las siguientes componentes es nulo:
Aquí hemos impuesto que I sea una dirección espacial distinta de J. Debido a ello, todas las componentes métricas que aparecen se anulan irremediablemente.
Ahora bien, ¿qué pasaría si intentásemos calcular este conmutador usando las ecuaciones de movimiento de las cuerdas y no estas reglas? Si la teoría es consistente tendría que dar el mismo resultado.
El conmutador de la cuerda abierta:
Las cuerdas abiertas tenían la siguiente ecuación de cuadriposición:
Aquí x0 sería la cuadriposición inicial y los coeficientes αnμ los generadores de vibraciones de modo n en la dirección μ.
Derivando respecto al tiempo:
Consideremos ahora el siguiente producto (que aparecía en la definición de M):
Vamos a necesitar integrarlo, para lo cual resulta muy útil tener en mente el siguiente par de reglas:
Aquí estamos usando la función delta de Kronecker, que vale 1 cuando las dos letras que lleva por subíndices son iguales.
Teniendo esto e integrando el producto que habíamos calculado obtenemos:
Aquí en el segundo paso hemos usado la delta de Kronecker para cargarnos un sumatorio.
Ahora bien, M tenía este término y otro igual cambiando de sitio μ y ν restando, con lo que combinando ambos el resultado final es:
Nótese que el término del medio, que era simétrico al incluir pμ pν multiplicados, desaparece. Por otra parte, en la última igualdad hemos hecho que el sumatorio solo barra los números naturales teniendo en cuenta que para valores negativos de n se obtenía lo mismo que para los positivos, y además hemos permutado los elementos del numerador, lo que ha causado el cambio de signo. Este tipo de cambios serán el pan de cada línea en esta entrada, con lo que conviene acostumbrarse a ellos y ser capaz de sobrellevarlos.
Teniendo este conmutador, podríamos decir ingenuamente que entonces nuestro objeto de interés M-I será:
Sin embargo, sucede que expresado así no es hermítico, un requisito indispensable para que sea un observable cuántico. Y no es hermítico porque x0I y p- no conmutan. Veamos por qué.
Recordemos las siguientes definiciones que involucran a los operadores L de Virasoro:
De la última línea se deduce directamente que p- es proporcional a L0, por tanto con lo que no conmute uno tampoco conmutará el otro. Y es relativamente directo demostrar que x0I y L0 no conmutan:
Debido a esto, la forma correcta de cuantizar M es hacer un apaño al término problemático sumándole su adjunto y dividiendo entre dos:
Y en esta expresión hay muchas cosas que si se mezclan no conmutan. Concretamente sabemos los siguientes conmutadores, siendo el último de Virasoro el más relevante al involucrar el número de dimensiones espaciales D como vimos en su momento:
Así pues, la cuenta que tenemos que hacer y verificar si es igual a 0 o no es la siguiente:
Por orden, denotaremos a los conmutadores que aparecen aquí como 1, 2, 3, 4, 5, 6, 7, 8 y 9. Pero antes de lanzarnos a la aventura, verifiquemos que esta cuenta sirve también para la cuerda cerrada.
El conmutador de la cuerda cerrada:
El movimiento de la cuerda cerrada venía dado por las siguientes ecuaciones:
La gran diferencia con las cuerdas abiertas eran los osciladores barrados, que indicaban pulsos propagándose en el otro sentido de la cuerda cerrada. De este modo, las cuerdas cerradas pueden poseer ondas estacionarias.
Si hacemos ahora el mismo producto que hicimos con la cuerda abierta obtenemos la siguiente barbaridad:
Para integrar esto, nuestras aliadas serán las siguientes reglas:
Con lo que obtenemos:
Y de nuevo, restando la otra parte, obtenemos que M para la cuerda cerrada es:
Cuantizando como antes, podemos deducir que M-I será:
Donde podemos hacer las siguientes sustituciones:
Y en esta expresión, si tenemos en cuenta que todo lo barrado conmuta con lo no barrado, tenemos claramente un duplicado de la expresión de la cuerda abierta, donde las cosas sin barra van por un lado y las que llevan barra van por el otro. Pero ambos grupos de conmutadores serían iguales que el de la cuerda abierta.
De modo que, en resumen, lo que obtengamos para la cuerda abierta será aplicable a la cuerda cerrada.
Comienzo de la cuenta kilométrica:
.-Conmutador 1:
El primer conmutador afortunadamente es nulo al no contener ninguna pareja de elementos que no sean conmutables:
.-Conmutadores 2 y 3:
En estos los únicos términos no conmutables son x0- y p+. Esto da como resultados:
.-Conmutadores 4 y 5:
Aquí sucede exactamente lo mismo que con los anteriores:
.-Conmutador 6:
Este ya es bastante más largo porque sus elementos x0 no conmutan con los L0 y hay que descomponerlo en otros ocho y hacerlos todos por separado. El resultado, muy gratificante, es que anula simultáneamente a los conmutadores 2 y 3:
Nótese que aunque las constantes fuera del paréntesis sean diferentes cancelará a los otros dos porque en la expresión donde aparecían cada uno tenía sus constantes extra. Esto solo es parte de lo que teníamos.
.-Conmutador 7:
Este va emparejado con el siguiente, pero es mejor separarlos. pues aquí lo único que conmuta es x0 con αn. Empezamos descomponiéndolo en otros cuatro conmutadores:
Y una vez hecho esto, podemos abordar cada uno de ellos por separado descomponiéndolo en otros tres y reordenando teniendo en cuenta aún más conmutadores:
De modo que en suma queda:
.-Conmutador 8:
A simple vista se aprecia que está relacionado con el anterior como lo estaban el 2 y 3, así como el 4 y el 5:
Recolocando el paréntesis, da exactamente el mismo resultado.
Descanso:
Recapitulando y sustituyendo, ahora mismo tenemos que nuestro conmutador ha adoptado la siguiente forma tras cancelar lo que se cancelaba y juntar estos dos últimos conmutadores:
Y dado que este conmutador sabemos que tiene que ser nulo, podemos simplemente escribir nuestra ecuación como:
Aquí hemos aprovechado la ocasión para «reordenar» L0, lo que daba lugar al término divergente d que ha sido añadido.
Llegados hasta aquí solo resta hacer ese pequeñito conmutador del último término, pero es una cuenta que requiere mucha paciencia y llevará más que todas las anteriores.
La larga batalla final del conmutador 9:
Empecemos deshaciéndolo en otros cuatro más pequeñitos:
.-Los cuatro conflictos principales:
Ahora, dado que en la ecuación principal aparece dentro de un doble sumatorio y dividido por n y m, haremos cada uno de estos cuatro sumándolo ya sobre n. Empezamos por el cuarto:
¿Hemos acabado con él? En absoluto. Ahora queda ver que el primer sumatorio puede ser apañado para quedar de otra forma a la que tal vez no proceda llamar «más simple»:
¿Qué hemos hecho aquí? Por orden:
- Descomponemos el sumatorio grande en cuatro sumatorios pequeños.
- Redefinimos n en el primero y en el cuarto, de forma que se parezcan respectivamente al segundo y al tercero.
- Le restamos el primer sumatorio al segundo y el cuarto al tercero.
- En el primer sumatorio, cambiamos n por -n.
- En el primer sumatorio separamos el caso n=0, en el segundo n=m y con lo que queda obtenemos el sumatorio de un conmutador.
- Desarrollamos el conmutador.
- Hacemos la suma, aplicando el criterio de suma de series de Gauss. Ya apareció aquí.
En suma, tenemos que:
El primer término se manipula de forma semejante, dando como resultado:
El segundo término es bastante más sencillo y se reescribe en tres pasos:
El tercer término, para concluir, se hace igual que el segundo:
Y juntando todo:
En el primer paso hemos escrito todos los resultados obtenidos por orden, añadiéndoles los coeficientes que quedaron ignorados desde que empezamos. En el segundo hemos agrupado y además ha pasado otra cosa muy importante. Al pasar L0 a la izquierda en los dos lugares en los que estaba ha sido necesario realizar dos conmutadores cuyo efecto ha sido cambiar, dentro del paréntesis grande, m-1 por m+1.
.-Los cuatro conflictos secundarios:
Una vez hecho esto, es posible añadir el segundo sumatorio dividiendo además por m. Eso sería equivalente a:
Y digo «sería» porque en los primeros términos he cambiado m por n aprovechándome de que es irrelevante. Ahora bien, ¿qué pasaría con el macrosumatorio doble final? Pues de nuevo lo sensato es dividirlo en cuatro cuentas diferentes y abordar cada una por separado.
En el primer paso, combinaremos los términos sexto y octavo:
Por orden, hemos:
- Redefinido m en el segundo sumatorio.
- Recolocado los osciladores en el segundo sumatorio.
- Restado.
- Separado el caso m=0.
El el segundo paso, combinaremos los términos primero y tercero:
Aquí hemos:
- Redefinido m en el primer sumatorio.
- Recolocado los osciladores en el primer sumatorio.
- Restado.
- Separado el caso m=n.
En el tercer caso, combinaremos los términos quinto y séptimo:
Aquí hemos:
- Redefinido m en el primer sumatorio.
- Pasado Lm al centro en el segundo, generando otro sumatorio porque no conmutan.
- Restado el segundo sumatorio al primero.
- Cambiado en el primero m por -m.
- Pasado Lm† al frente en el primero, generando otro sumatorio porque no conmutan.
- Separado el caso m=0 en el primero. En el segundo, realizamos la suma.
Por último, en el cuarto caso, combinamos los términos segundo y cuarto:
Y aquí hemos:
- Redefinido m en el segundo sumatorio.
- Pasado Lm† al centro en el primero, generando otro sumatorio.
- Restado el segundo sumatorio al tercero.
- Cambiado m por -m en el segundo.
- Pasado Lm a la derecha en el segundo, generando otro sumatorio.
- Sumado en el segundo. Separado el caso m=0 en el tercero.
- Pasado L0 a la izquierda en el tercero.
Combinando todo:
El primer término obtenido se carga el aporte de los conmutadores 7 y 8, dejando solo el factor divergente d. El segundo término, por otra parte, se carga el aporte de los conmutadores 4 y 5.
El último término, que queda un poco marginado, puede reescribirse con un poco de cuidado. Si nos fijamos, todos los osciladores tienen por índice n+m, de modo que podríamos redefinir n como n+m y sumar para todos sus posibles valores: el valor 1 saldría cero veces, porque n y m valen 1 como poco, el valor 2 saldría una vez, el valor 3 saldría dos veces (n=2 m=1 y n=1 m=2), y en general, el valor n-ésimo saldrá n-1 veces, con lo que:
Y teniendo el último término escrito así, el conmutador 9 finalmente toma la forma:
El anhelado final:
Sustituyendo nuestra expresión para el sumatorio del conmutador 9 en la ecuación que teníamos igualada a cero y cancelando todo lo cancelable, nos queda lo siquiente:
De modo que para que el conmutador de M analizado sea nulo tiene que cumplirse la última igualdad. Y como tiene que ser cierta para cualquier valor de n, necesariamente deben seguirse las siguientes condiciones:
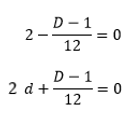
Lo cual implica que nuestra teoría básica de cuerdas requiere de 25 dimensiones espaciales y un factor divergente igual a -1:
¡Meta alcanzada!
Comentarios sobre el factor divergente:
A partir de su definición, este era exactamente:
De donde se deduce, usando los valores obtenidos, que según la teoría de cuerdas la suma de todos los números naturales da como resultado:
Pero afortunadamente esto no nos pilla por sorpresa, dado que ya dedicamos una entrada a explicar cómo podría justificarse tal conclusión.
En la próxima entrada veremos que precisamente gracias a que la teoría de cuerdas tratada suma así, es capaz de reproducir fotones y gravitones.
Categorías:Física, Teoría de Cuerdas































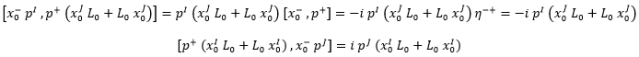



























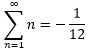
Voy a dejarlo «pa prao».
Estudie y aprendi un poco de ecuaciones lineales de primer grado y ecuaciones cuadraticas, pero esto que acabo de leer, me parece sorprendente, el universo en si, es sorprendente
no entendi ni madres pero se ve hermoso *-*