La relatividad especial nos permite comparar las mediciones que hacen dos observadores independientes de las mismas magnitudes cuando entre ambos hay una cierta velocidad relativa v mediante las transformaciones de Lorentz. Dichas transformaciones solo se pueden aplicar con tranquilidad cuando la velocidad relativa es uniforme y no varía en el tiempo.

Si la velocidad entre los dos observadores varía y, por tanto, hay una aceleración relativa a, será posible siempre aplicar instantáneamente una transformación de Lorentz considerando la velocidad instantánea. Sin embargo, dicha operación nos dará una relación puntual entre las medidas y no podrá extrapolarse en el tiempo.

En suma, las aceleraciones van a alterar el concepto de derivada y por tanto magnitudes que son invariantes en relatividad especial dejan de serlo. De esta idea, en combinación con la asignación de un sistema de referencia privilegiado al vacío, surge toda la relatividad general.

En esta entrada veremos cómo un movimiento acelerado rompe las simetrías de la relatividad especial creando una diferencia entre los dos observadores, haciendo a uno de ellos privilegiado y al otro inconsciente de que está padeciendo una deformación del espacio-tiempo. Esta observación, realizada por Einstein en 1907 en su conocida paradoja de los gemelos, le llevó a desarrollar la teoría de la relatividad general.

Repaso de relatividad especial:

Usando unidades naturales, la cuadrivelocidad U de un cuerpo con velocidad v se define como:

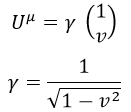
Aquí γ era el factor de dilatación de Lorentz.

Para hacer un producto escalar entre cuadrivectores del espacio vacío se usa la métrica de Minkowski η, es decir, se multiplican las componentes temporales y se les resta el producto de las componentes espaciales:

Aplicando esto, el módulo de la cuadrivelocidad siempre es 1:

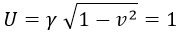
La velocidad podía escribirse en función de la rapidez φ mediante una tangente hiperbólica:

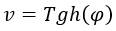
Cumpliéndose además las siguientes relaciones:

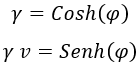
Con lo cual podemos reescribir la cuadrivelocidad y su módulo como:

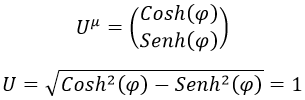
La cuadriposición, por suparte, venía dada por la integral de la cuadrivelocidad en el tiempo propio del cuerpo en movimiento τ:

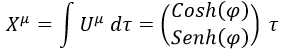
De forma que el módulo de la cuadriposición coincidía con el tiempo propio:

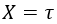
Esto último veremos que no es correcto cuando haya aceleraciones, y que solo preservaremos que la variación de tiempo propio será igual al módulo de la variación de la cuadriposición.

Cuadriaceleración y su módulo:

Supongamos que tenemos un vector de velocidad v dado por:

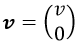
Y que, a su vez, tenemos un vector aceleración a con una componente paralela a la velocidad y otra perpendicular:

La cuadrivelocidad tendría la siguiente forma:

Y para obtener la cuadriaceleración tendríamos que derivarla respecto al tiempo propio. Sin embargo, v y a son la velocidad y aceleración respecto al tiempo de observador, con lo que nos vemos obligados a emplear la regla de la cadena.

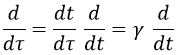
También necesitaremos la derivada del factor de Lorentz respecto al tiempo de observador:

Aquí aparece solo la aceleración paralela a la velocidad por ser la única que modifica su módulo. Las aceleraciones perpendiculares al movimiento inducen giros pero no alteran la velocidad.

Teniendo esto en cuenta, la cuadriaceleración A resulta ser:

Y su módulo:

A raíz de esto último, cabe destacar que la cuadriaceleración siempre será tipo espacio (módulo complejo).

Movimiento uniformemente acelerado:

Supongamos que un observador percibe un cuerpo moverse con una aceleración uniforme. En mecánica clásica esto implicaría que con el paso del tiempo su velocidad acabaría siendo infinita. Sin embargo, en mecánica relativista la velocidad máxima es la de la luz, es decir, 1. La «velocidad» que puede aumentar indefinidamente en términos relativistas es la rapidez. A tales efectos, aquí llamaremos aceleración uniforme a la aceleración de la rapidez α:

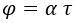
Si consideramos la variación de rapidez que van midiendo simultáneamente todos los observadores que coinciden con el cuerpo (y por tanto comparten tiempo propio), todos ellos perciben la misma aceleración.

Usando esta expresión, podemos decir que la cuadrivelocidad será:

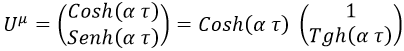
E integrando y derivando respecto al tiempo propio podemos sacar la cuadriposición y la cuadriaceleración:

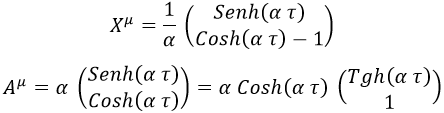Aquí cabe destacar que en la cuadriposición restamos 1 en la componente espacial para que inicialmente sea nula, beneficiándonos para ello de la constante de integración.

Haciendo una comparativa entre todas estas expresiones para los cuadrivectores y las vistas en la sección anterior, se puede llegar a las siguientes relaciones entre ambas nomenclaturas:

Aquí se puede apreciar que el tiempo y la posición se disparan hacia infinito a media que pasa el tiempo propio, que la velocidad y la rapidez se relacionan de la forma usual, teniendo la primera a la velocidad de la luz a medida que pasa el tiempo y, por último, que la aceleración observada cada vez se hace más pequeña hasta ser prácticamente nula.

Algo digno de destacar, por otra parte, es que tal y como anticipábamos el módulo de la cuadriposición deja de coincidir a priori con el tiempo propio, salvo en el instante inicial en que ambos son nulos.

Geometría del movimiento acelerado:

Teniendo en cuenta que en relatividad general todas las aceleraciones se explican como una adaptación a la forma del espacio-tiempo, cabe preguntarse si podemos reducir a tales términos un movimiento acelerado uniforme.

Empecemos pensando en la relación entre las coordenadas t y x del observador del cuerpo acelerado y las coordenadas τ y x’ del cuerpo en cuestión. Acabamos de ver que dicha relación sería:

Esto sería cómo un observador externo obtendría sus coordenadas teniendo las del cuerpo. En la sección anterior fijamos x’ nulo. Este observador externo, que preventivamente decimos que está en reposo absoluto, observará la geometría del espacio-tiempo que afecta al cuerpo. Ambos, observador y cuerpo, parten del mismo punto.

Pero a la vez que el observador ve al cuerpo padecer una aceleración que lo arrastra, el propio cuerpo, que no puede percibirla por el principio de equivalencia, ve al observador padecer una aceleración hacia atrás que lo aleja indefinidamente. El cuerpo, por otra parte, ignora la geometría del espacio-tiempo. En su sistema de coordenadas, el observador se mueve hacia atrás según:

Aquí simplemente hemos despejado de las relaciones anteriores.

Ahora bien, sabemos que en las coordenadas τ y x’ la geometría es minkowskiana. Con lo cual, si las tenemos expresadas según t y x y reobtenemos la métrica podremos percibir cómo se ha deformado la percepción del espacio-tiempo.

Para obtener la métrica, en primer lugar hay que derivar la cuadriposición respecto a t y x por separado. Lo primero es equivalente a calcular la cuadrivelocidad del observador respecto al cuerpo, en tanto que su tiempo propio es t:

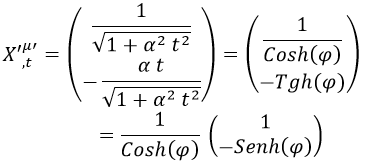
Comparando la última expresión con la fórmula de la cuadrivelocidad, podemos ver que según el cuerpo el observador se mueve hacia atrás con velocidad ilimitada:

Esto es una clara señal de que el cuerpo está midiendo una realidad deformada sin darse cuenta, ya que es imposible que la velocidad del observador acabe superando a la de la luz.

Por otra parte, la derivada de la cuadriposición respecto a x es:

Con lo que la métrica deformada g toma la forma:

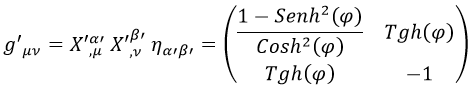
Cabe destacar que esta métrica carece de curvatura de Ricci al ser una simple transformación de coordenadas de la métrica plana. Un espacio-tiempo que induce aceleraciones uniformes en una dirección concreta es una percepción deformada de uno vacío.

Hay que destacar que esta métrica es de la forma adecuada para que la cuadrivelocidad medida por el observador siga dando como resultado 1:

Y, consecuentemente, el tiempo propio se sigue pudiendo calcular como la integral de la variación de la cuadriposición.

Dificultad para percibir diferencias entre un cuerpo acelerado y otro que percibe aceleración:

En la sección anterior hemos demostrado que es muy diferente padecer aceleración que observarla. Las conclusiones del cuerpo que padece aceleración y piensa que es el resto del mundo el que va al revés llegaban a ser absurdas.

El motivo por el que es tan complicado discernir entre ambas situaciones en la vida cotidiana es que es necesario tratar con velocidades próximas a la de la luz para percibir diferencias. Y para muestra, resulta que si hacemos la serie de Taylor respecto al tiempo de las cuadriposiciones identificadas por el observador y el cuerpo respecto del otro, vemos que a tiempos pequeños no hay ninguna diferencia perceptible (cada uno ve al otro llevando un movimiento uniformemente acelerado en sentido clásico en la dirección contraria):

Conclusiones:

Para poder dar sentido a las ecuaciones de los cuadrivectores acelerados en un contexto relativista es necesario indicar qué observador es privilegiado (percibe la geometría a la que está sometido el otro) y cuál no. Esto no se puede hacer al azar, sino que requiere de un criterio o de mediciones en tiempos prolongados.

En suma, requiere relatividad general. El observador sometido a aceleración «real» no percibe la geometría y el sometido a aceleración ficticia sí la percibe.

Hablamos, de hecho, de la explicación teórica a la paradoja de los gemelos, ya explicada en esta entrada. Si el de la nave envejece menos no es por la velocidad sino porque imponemos que es la nave la que se acelera alejándose de la Tierra y no la Tierra la que se acelera alejándose de la nave.