2. TEORÍA DE CAMPOS UNIDIMENSIONAL

2.1. La energía potencial
2.2. La conservación de la energía
2.3. La gravedad de Galileo
2.4. El trabajo y el calor

Relación entre fuerza y energía potencial.

En el capítulo anterior obtuvimos matemáticamente, a partir de la energía potencial, la ecuación de movimiento que describía el movimiento de un cuerpo sometido a la gravedad de Galileo, pero quedó todo explicado como simples pinceladas. En este capítulo, por el contrario, veremos toda la estructura matemática que hay por detrás en detalle y en qué medida se puede generalizar el proceso para otras energías potenciales.

En primer lugar, partiremos siempre de la ecuación de la energía, en la cual vamos a indicar esta vez que la energía cinética típicamente dependerá de la velocidad v y la potencial de la posición x. Esto se indica con un paréntesis tras cada una:

La energía cinética, dentro del marco clásico en el que nos movemos, siempre tendrá la misma expresión, con lo que también es válido partir de:

A partir de la expresión de la energía, siempre podremos obtener la ecuación de fuerzas vivas, que indica que la variación de energía cinética es opuesta a la de energía potencial:

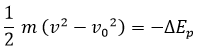
Llamaremos a estas dos ecuaciones, la de la energía y la de las fuerzas vivas, ecuaciones de estado del sistema. Esta nomenclatura es personal, aunque la heredo de la termodinámica, y tan solo servirá para que nos entendamos a lo largo de este capítulo. Lo que las va a caracterizar es que no es necesario derivar ni integrar para obtenerlas, y que no dependen del tiempo.

Derivando la ecuación de la energía respecto al tiempo teniendo en cuenta que tiene que dar 0, y aplicando la regla de la cadena, siempre obtendremos lo siguiente:

La expresión final, tras simplificar los doses y eliminar las velocidades, nos va a dar lugar a la siguiente ecuación diferencial de movimiento:

La cual se lee así: «el producto de la masa por la aceleración siempre es opuesto a la derivada de la energía potencial con respecto a la posición«. ¿Os suena algo? A Newton el producto de la masa por la aceleración le parecía una magnitud tan importante que decidió darle un nombre técnico: fuerza.  Y la segunda ley de Newton, un clásico, dice precisamente que una cosa es igual a la otra.

Ahora bien, si cambiamos el producto m a por una F de fuerza, la ecuación a la que hemos llegado toma el siguiente aspecto:

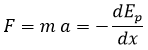
Fijaos bien en lo que esto significa: «las fuerzas que padecen los cuerpos siempre se oponen a la derivada de la energía potencial con respecto a la posición«. Dicho de otra forma, si tenemos una cierta energía potencial que aumenta en una dirección concreta, la fuerza que padecerá un cuerpo sometido a ella le empujará en la dirección opuesta. Si la energía potencial aumenta con x, la fuerza será negativa y empujará hacia el lado opuesto. Si la energía potencial disminuye con x, la fuerza será positiva y empujará en esa dirección.

En suma, cuando decíamos que el principio de mínima energía establece que todos los cuerpos huyen de la energía potencial, otra forma de enfocarlo es decir que los cuerpos padecen fuerzas que les guían en el sentido en la que la energía potencial se reduce lo máximo posible. El sentido que reduce lo máximo posible la energía potencial, si esta cumple propiedades habituales como ser derivable (o diferenciable) y continua, será el opuesto al sentido en el que aumenta lo máximo posible.

Es difícil volver a ver las fuerzas con los mismos ojos tras comprender este hecho. Que la fuerza gravitatoria tire de los cuerpos hacia abajo únicamente significa que la energía potencial se reduce en esa dirección. ¿Existe la fuerza? ¿Existe la energía potencial? Ambos, en realidad, son conceptos que usamos para describir cómo se van a mover los cuerpos.

A partir de la ecuación diferencial del movimiento, o de la de la fuerza, es posible recuperar la ecuación de las fuerzas vivas mediante el truco de expresar la aceleración usando la regla de la cadena. Veamos en unos pocos pasos (integración mediante) cómo funcionaría el asunto:

Así comprobamos que, pese a haber derivado, integrando podemos recuperar la misma información original. En esencia de todas las ecuaciones tiene que poderse concluir lo mismo.

Si quisiéramos recuperar la expresión de la energía potencial conociendo la fuerza, por otra parte, simplemente tendríamos que realizar la siguiente integral sin límites:

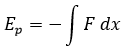
Baste decir, para concluir esta sección, que conocer la fuerza y conocer la energía potencial es más o menos equivalente, y por eso se da la circunstancia de que en muchos centros los estudiantes aprenden únicamente a trabajar con fuerzas, desconociendo en gran medida el poder de cálculo que tiene la energía. Sin embargo, trabajar con energías tiene una clara ventaja frente a trabajar con fuerzas, y es que nunca aparecen vectores.

Ecuaciones de la velocidad y la posición.

En el capítulo anterior vimos en detalle que había dos formas diferentes de llegar hasta la velocidad. Una de ellas consistía en partir de la ecuación de las fuerzas vivas y despejarla en función de la variación de energía potencial:

Y la otra consistía en integrar la aceleración en el tiempo:

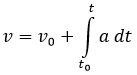
En lo referente a la posición, también podíamos calcularla de dos formas, según cómo hayamos obtenido la velocidad. Eran las siguientes:

Una vez que conocemos la dependencia entre la posición y el tiempo, la cual sería la ecuación integral del movimiento, es muy fácil llegar a la ecuación diferencial del movimiento derivando dos veces y, a partir de ahí, reiniciar todo el proceso:

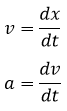
Cambios entre ecuaciones.

En general, derivar es más fácil que integrar. En particular, derivar siempre es posible, pero integrar puede ser imposible porque la función tal que derivada da la que tenemos no se pueda escribir en términos de otras funciones conocidas.

Esto tiene una consecuencia directa. Si tenemos la ecuación integral del movimiento, x(t), siempre vamos a poder derivarla dos veces para obtener v(t) y a(t), pero quizás después resulte imposible obtener Ep(x) integrando la fuerza (m a(t)). Del mismo modo, si conocemos la energía potencial Ep(x) siempre será posible que calculemos la fuerza, y con ella la aceleración, pero a lo mejor no es posible obtener finalmente la ecuación x(t). En resumen, siempre podremos obtener la aceleración y la fuerza, pero todo lo demás depende de la suerte (de lo complicado matemáticamente que sea el problema).

El siguiente esquema ilustra lo que estamos exponiendo aquí. Las líneas verdes indican operaciones garantizadas, mientras que las rojas pueden ser imposibles de realizar.

Los senderos verdes son cambios de ecuaciones que siempre podemos hacer, ya que involucran operaciones habituales o derivadas, que no pueden no dar solución en condiciones normales. Todos tienen marcada al lado la ecuación que los caracteriza. Los senderos rojos involucran integrales, y por tanto no están garantizados. Por último, los senderos naranjas a trazos requieren, o bien conocer x(t), o bien conocer t(x), además de la ecuación que se quiera cambiar.

Trabajo termodinámico.

En física, denominamos como trabajo (W) a la integral de la fuerza a lo largo del eje de movimiento entre dos posiciones dadas. El trabajo, que tiene unidades de energía, no es un tipo de energía, sino una medida de cuánto ha variado esta. Podemos comprobar fácilmente que el trabajo, por su definición, es equivalente a la variación de energía cinética, y por consiguiente opuesto a la variación de energía potencial:

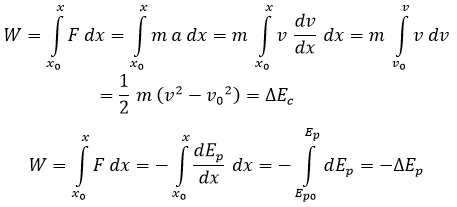
Como el trabajo solo depende de la variación de energía potencial entre el punto inicial y el punto final del trayecto, es irrelevante conocer la ruta que sigue el cuerpo mientras se mueve con detalle. Podemos calcularlo conociendo únicamente dónde empieza y dónde acaba. En particular, cabe destacar que si un cuerpo comienza a moverse y acaba en un mismo punto, el trabajo realizado sobre él es de 0 J, ya que su energía potencial será la misma.

Un cuerpo de 3 kg comienza a caer afectado por la gravedad de Galileo desde 70 m de altura. ¿Cuánto trabajo ha realizado sobre él la gravedad cuando llega a los 40 m de altura?

Para resolver esto, simplemente tenemos que calcular el opuesto de la variación de energía potencial:

Potencia termodinámica.

Junto al concepto de trabajo, también suele ser útil definir el de potencia (P), que no es otra cosa que la derivada del trabajo respecto al tiempo. Se puede demostrar rápidamente que tiene que coincidir con el producto de la fuerza por la velocidad:

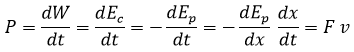
Como se puede ver, la potencia también se puede entender como la derivada de la energía cinética respecto al tiempo.

Presuntas pérdidas de energía.

Desde que está establecida como ley la conservación de la energía, la cual es además el primer principio de la termodinámica, nunca ha faltado gente dispuesta a desmentirlo «mostrando» que podían producir energía de la nada. En general, todas las máquinas que conseguían tal proeza caían han caído en dos categorías a lo largo de la historia: o bien eran engaños, o bien quien las inventó no era consciente de una fuente de energía extra que era la que hacía que apareciese.

Vamos a entender esto con un ejemplo muy sencillo, que es el de la caída libre. Pongamos por caso que yo suelto un cuerpo en el aire y considero que mi sistema físico solo está formado por ese cuerpo, sin la gravedad. En cuanto el cuerpo empiece a ganar energía cinética al caer, yo podría decir que está apareciendo energía de la nada. Pero nada más lejos de la realidad: lo que sucedería es que he ignorado completamente la presencia de la energía potencial gravitatoria, la cual se está reduciendo para que el cuerpo pueda ganar cinética.

Siempre que la conservación de la energía ha parecido fallar, tras ser analizado el problema con detalle ha llevado a un nuevo descubrimiento. Por ejemplo, desde que sabemos que la luz transporta energía podemos comprender de qué se nutre nuestro planeta para que sigan sucediendo cosas: del Sol. También hay una parte de la energía de la Tierra que nace de la física del núcleo, pero no entraremos en esos detalles ahora.

En los años 20, como veremos al llegar al bloque de fenómenos cuánticos, parecía que cierto tipo de desintegración nuclear llamada beta a veces suponía la desaparición de energía, pero en realidad lo que sucedía era que los físicos estaban perdiendo el rastro de una partícula hasta entonces desconocida: el neutrino. Actualmente, la conservación de la energía sigue dando problemas cuando analizamos el universo, llevándonos a la hipótesis de que tiene que haber un montón de materia y energía oscura rodeándonos.

La cuestión es que cuando hacemos física tenemos que tener claros tres conceptos:

• Nuestro sistema es aquello con lo que trabajamos directamente y tomamos en consideración.
• Los sistemas internos son aquellos subsistemas que forman parte de nuestro sistema, pero no son analizados en detalle. Por ejemplo, cuando consideramos los objetos como puntos, estamos ignorando toda la física que hay en su estructura interna.
• Por último, los sistemas externos son aquellos que no consideramos en absoluto y que pueden, o no, afectar a nuestro experimento.

Es importante recalcar que la clasificación depende de quien esté analizando el sistema, y lo que para uno es parte del sistema, para otro puede ser sistema interno u externo. Por ejemplo, en el caso del cuerpo cayendo, quien considere la gravedad desde el principio la tendrá como parte del sistema, pero quien la obvie la percibirá como sistema externo.

Ignorar los sistemas externos que afectan al nuestro puede llevar (y lleva) a la gente a concluir que en su sistema la energía aparece o desaparece de la nada. De verdad os sorprendería la cantidad de gente, particularmente en internet, que asegura haber encontrado la máquina de movimiento perpetuo con este tipo de errores conceptuales. Recuerdo ahora mismo un caso de uno que aseguraba que la energía evidentemente se podía crear de la nada porque era lo que hacían las pilas (cuando en realidad convierten energía electromagnética en cinética (corriente)).

Calor y temperatura.

Ahora bien, ¿qué sucede cuando tenemos un subsistema que sabemos que está ahí, pero no podemos o no queremos molestarnos en analizarlo en detalle? Bienvenidos al fantástico mundo de las aproximaciones estadísticas.

Un solo gramo de agua contiene mucho más que millones de millones de electrones, protones y neutrones, entre otras partículas. Para analizar el movimiento de una gota de agua podríamos considerar toda esta cantidad colosal de partículas, sus posiciones y sus movimientos, o podemos considerar que nos dan igual en realidad y que podemos tratar la gota como si fuese un punto.

Si elegimos lo segundo, que será lo habitual muchas veces, estaremos ignorando voluntariamente un montón de energía cinética debida a las partículas constituyentes de la gota. Llamamos temperatura a una forma de medir la cantidad de movimiento que tienen las partículas de los sistemas internos, y cuanto mayor es esta más energía cinética tienen dichas partículas.

Lo relevante al nivel en el que estamos es que, en ocasiones, nuestro sistema podrá perder o ganar energía según aumente o disminuya la temperatura de sus constituyentes. Si nuestro sistema gana energía, es que sus constituyentes han reducido su temperatura liberando calor, que como el trabajo, no es más que una transferencia de energía.  Por el contrario, si la pierde, es que sus constituyentes han aumentado su temperatura absorbiendo calor.

Esto se ve muy claro con el siguiente ejemplo. Cogemos un cuerpo, lo soltamos y lo dejamos caer al suelo. Al soltarlo, tiene un montón de energía gravitatoria, pero cuando llega al suelo y choca no tiene ni energía gravitatoria ni cinética porque está quieto. ¿Dónde se ha ido toda esa energía? En calor. La colisión ha aumentado la temperatura del suelo y del objeto, esto es, sus partículas se han comenzado a mover más rápido, e incluso habrán roto sus estructuras internas en el caso de que algo se rompa.

Podemos medir el calor Q como la energía nueva que aparece en el sistema:

Si se gana energía cinética y potencial, el calor será negativo, indicando que se habrá reducido la energía de los subsistemas. Si ambas se reducen, será porque el calor ha sido positivo y los subsistemas han aumentado su temperatura.

Dejamos caer una pluma desde una altura de 3 m, y esta llega al suelo con una velocidad de 0,06 m/s. ¿Cuánta energía se ha disipado por calor, es decir, chocando con el aire, si su masa es de 0,00001 kg?

El calor resulta ser positivo, pero pequeñito. Eso significa que la temperatura del sistema (concretamente del aire) habrá aumentado un poco mientras la pluma caía.

Por último aquí, es muy importante aclarar que si en un sistema se producen ganancias o pérdidas por calor, deja de ser correcto el teorema de las fuerzas vivas y es necesario emplear la fórmula que incluye el calor en su lugar.

Y, concluido este capítulo, ya hemos aprendido un montón en lo referente a la teoría de campos unidimensional y su estructura matemática. Próximamente continuaremos con ejemplos más útiles de su aplicación, como son los muelles, la gravedad de Newton o la electrostática de las cargas.

No obstante, antes de todo eso, en el próximo capítulo hablaremos acerca de las aproximaciones en física en detalle. ¿Cuándo podemos aproximar? ¿Cómo? ¿En qué medida son fiables los resultados cuando hacemos aproximaciones? Estas cuestiones son muy relevantes para saber cuándo podemos emplear unos modelos u otros y para trabajar en laboratorio, donde los resultados no solo deben tener un valor sino que además se tiene que indicar en qué medida dicho valor es fiable.

ACTIVIDADES PROPUESTAS
1. Dos coches se cruzan en sentidos opuestos por la carretera. Uno tiene una masa de 1500 kg y circula a 30 m/s. El otro, conducido por alguien más temerario, tiene una masa de 1300 kg y circula a 50 m/s. Por culpa del segundo conductor, ambos coches colisionan frontalmente y acaban en reposo. ¿Cuánto sumaban sus energías cinéticas inicialmente? ¿Cuál es el calor asociado al choque? ¿Se absorbe o se emite? Describe las transformaciones energéticas que están involucradas en este suceso.
2. Tenemos una energía potencial cuya expresión es Ep=k*x^3, donde * representa una multiplicación, es decir, es igual a una constante k multiplicada por el cubo de x. Obtén la expresión para la fuerza en función de x, esto es, F(x).
3. Demuestra que en un movimiento rectilíneo uniforme, donde x=v*t, no hay aceleración derivando dos veces con respecto al tiempo.
4. Dejamos caer un cuerpo de 9 kg desde una altura de 25 m, sometido a la gravedad de Galileo.
a) Demuestra derivando que la fuerza a la que está sometido es F=-m*g.
b) ¿Cuánta velocidad tiene cuando x=10 m?
c) ¿En cuánto tiempo alcanza esa altura?
d) ¿Qué potencia ejerce la gravedad sobre él en ese momento?