Con la reciente detección de las ondas gravitatorias, ha despertado un interés más o menos escondido entre los aficionados a la ciencia, y es el de cómo se calcula la radiación que emiten los cuerpos y cómo esta es respetuosa (o no) con el principio de conservación de la energía. A tales efectos, he decidido dedicar una serie de entradas a cómo se calculan las ondas gravitatorias emitidas por un par de agujeros negros en rotación, combinándolas técnicas como esta y divulgativas.

No obstante, antes de entrar de lleno en el tema empezaré, como es habitual, dando un rodeo y pasando primero por la versión del electromagnetismo, más sencilla. En esta ocasión hablaré de energía electromagnética y su radiación, planteando al final algo que podría considerarse una paradoja (y que de hecho en un contexto clásico lo es). Posteriormente, hablaré de transformaciones relativistas de campo electromagnético y la radiación Larmor. Más tarde, publicaré las primeras entradas sobre electrodinámica cuántica a un nivel un poco más serio que cuando la planteé de forma heurística. Por último, nos adentraremos en cómo aplica todo esto cuando tratamos con gravedad.

En cualquier caso, aclaro que esto no será lo único de lo que hable próximamente, sino que simplemente habrá una serie de entradas orientadas en esa dirección.

Repasando ingredientes del electromagnetismo:

La densidad lagrangiana del campo electromagnético en interacción con cargas, que presentamos en su momento, puede escribirse del siguiente modo:

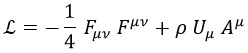
Aquí F era el campo electromagnético, ρ la densidad de carga, U la cuadrivelocidad de las cargas y A el cuadripotencial electromagnético, definido como. El campo electromagnético era la derivada exterior del cuadripotencial:

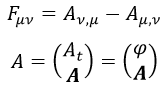
Aquí φ es el potencial electrostático y las comas representan derivadas parciales. Las magnitudes en negrita en las ecuaciones son vectores espaciales euclídeos.

Los campos eléctrico E y magnético B, por su parte, se definían a partir de F y A del siguiente modo:

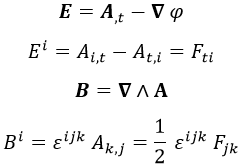
Aquí ε es el símbolo alternante de Levi-Civita. Las ecuaciones con índices evidentemente no son tensoriales en la primera igualdad, al cambiar el índice de arriba a abajo.

Si consideramos que el primer índice marca las filas y el segundo las columnas, podemos escribir el tensor F de los siguientes modos:

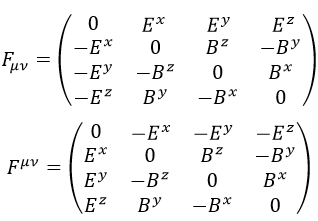
La contracción de F consigo mismo, que aparecía en la lagrangiana, no es más que la suma de los productos de cada uno de los términos de una matriz con el asociado de la otra, y da como resultado:

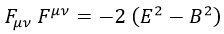
Por otra parte, el momento asociado al cuadripotencial es el propio campo electromagnético con signo invertido:

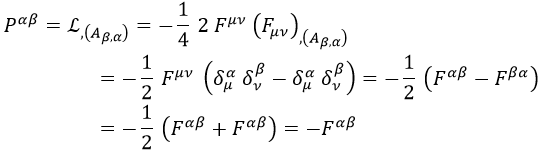
Y con esto ventilamos el repaso mínimo de partida.

Energía electromagnética:

Teniendo todos los ingredientes anteriores y aplicando la teoría de Hamilton, podemos construir la densidad de energía electromagnética como la suma de los momentos que tengan como alguna componente t multiplicados por su derivada del cuadripotencial asociada, restando posteriormente la lagrangiana. Resulta así que la densidad de energía electromagnética u es:

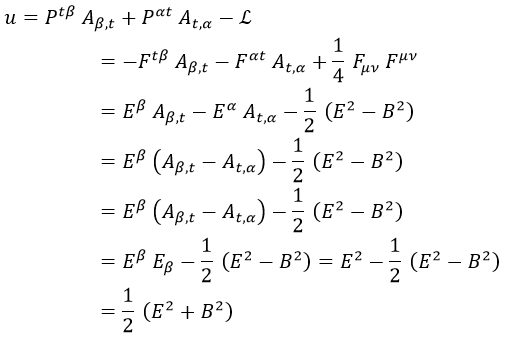
Es decir, que campo eléctrico y magnético contribuyen del mismo modo a la energía del campo. Cabe destacar que a efectos de ecuaciones, es «como si» el campo eléctrico fuese la energía cinética del campo y el magnético la potencial. En teoría de cuerdas esta lectura tiene una aplicación mucho más práctica, como veremos en su momento.

Las ecuaciones de Maxwell y el teorema de Poynting:

Una vez que conocemos la densidad de energía electromagnética, podemos preguntarnos qué puede causar que esta varíe con el tiempo. Es decir, ¿qué hace que en un cierto volumen del espacio se pierda o gane dicha energía?

Para ello, es conveniente recordar las ecuaciones rotacionales de Maxwell:

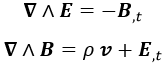
Y una vez que tenemos esto, derivamos respecto al tiempo la densidad de energía a ver qué sucede:

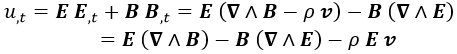
Aquí en la segunda igualdad hemos despejado las derivadas temporales de los campos usando las ecuaciones rotacionales de Maxwell.

El último término de la ecuación es el producto de la densidad de fuerza eléctrica por la velocidad de las cargas, con lo que es la densidad de potencial eléctrica wE,t:

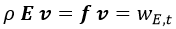
Por otra parte, si definimos el vector de Poynting S como:

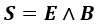
Se cumple que su divergencia es opuesta al otro término obtenido:

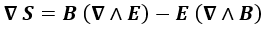
Combinando estos resultados, podemos expresar el teorema de Poynting diferencial del siguiente modo:

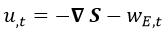
Es decir: las pérdidas de energía electromagnética en un cierto volumen del espacio son producidas por las «fuentes de Poynting» y el trabajo eléctrico. Lo segundo es lo esperable: el trabajo eléctrico transforma energía electromagnética en energía cinética de las cargas, ¿pero qué son las fuentes de Poynting? Desde luego no formaban parte de la mecánica clásica (téngase en cuenta que este teorema data de 1884). ¿En qué se convierte esa energía?

Acabamos de demostrar nada más y nada menos que las ondas electromagnéticas, como la luz, pueden transportar energía. Esto no es novedoso teniendo en cuenta que es un resultado obvio de la relatividad especial, pero tanto esta como el efecto fotoeléctrico son de 1905, posteriormente.

Integrando la ecuación anterior en el volumen y aplicando el teorema de Gauss, obtenemos el teorema de Poynting integral:

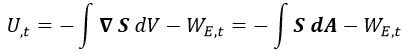
De aquí podemos concluir que para que la energía electromagnética escape como tal de un volumen es necesario que su vector de Poynting sea no paralelo a la superficie que lo encierra.

Algunas consecuencias:

Supongamos que tenemos una carga en reposo. El campo eléctrico de la misma saldrá en todas direcciones en línea recta y no habrá campo magnético puesto que tendrían que ser perpendiculares y preservar la simetría esférica en todo momento, siendo ambas cosas incompatibles.

Al no haber campo magnético, el vector de Poynting es nulo y por tanto es imposible que una carga radie campo electromagnético. Sin embargo, para que una carga atraiga a otra tiene que comunicarle el electromagnetismo de algún modo. ¿O acaso es la fuerza electrostática una interacción instantánea que no requiere de una energía intermedia?

La respuesta es que, como ya explicamos en su momento, la naturaleza se beneficia del principio de incertidumbre de Heisenberg para transmitir energía electromagnética de forma «ilegal» en tiempos en los que esta no puede ser observada.