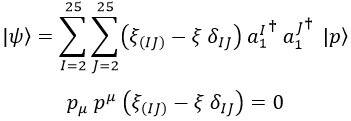Esquema de las escalas de la materia. En la figura 1 tenemos un diamante. En la figura 2 tenemos su estructura molecular. En la figura 3/4 tenemos uno de sus átomos de carbono. En la figura 5 tenemos los quarks dentro de uno de sus nucleones. Por último, en la figura 6, estarían las cuerdas que darían lugar a electrones y quarks.
Durante las últimas entradas hemos hablado de cuerdas relativistas y analizado cómo se podrían mover. Después cuantizamos sus vibraciones y vimos que había un problema con el número de dimensiones. Dicho problema fue analizado en detalle al respecto durante la última entrada sobre el tema, donde llegamos a la conclusión de que las cuerdas cuantizadas necesariamente tendrían que vivir en 25 dimensiones espaciales.
Sin embargo, pese a que hicimos todas esas cuentas no vimos en detalle por qué podría merecer la pena tirar para delante con ellas en lugar de simplemente desechar la teoría. Todo comenzó, como resumimos, debido a que Veneziano descubrió que las fuerzas entre los componentes de los protones y neutrones tenían la misma estructura matemática que las fuerzas debidas a la tensión de una cuerda.
No obstante, la teoría tomó fuerza no como una posible explicación de la interacción fuerte sino como una posible explicación de la gravedad cuántica, dado que en ella los gravitones estaban completamente a la orden del día. Y eso es lo que veremos en esta entrada: que las cuerdas cuantizadas vibrando pueden generar estados cuánticos con las propiedades de la gravedad entre otras opciones.
La teoría de cuerdas como una teoría sobre la estructura de las partículas:
El Modelo Estándar de la física de partículas supone que todos sus ingredientes son puntuales, es decir, que no ocupan un volumen en el espacio. Sin embargo, la mayoría de las partículas tienen una magnitud asociada llamada espín que representa matemáticamente una especie de giro interno de las mismas. Pero un punto no puede girar, de modo que o el espín es un concepto que se escapa completamente a nuestra comprensión intuitiva o las partículas realmente tienen una estructura, solo que esta es inferior a nuestra capacidad de medida.
En la teoría de cuerdas esta cuestión se salva diciendo que todas las partículas en realidad son pequeñas cuerdas vibrando y que con sus vibraciones generan todo cuanto observamos. ¿Cómo de pequeñas serían dichas cuerdas? Pues como poco más pequeñas que lo que observamos y, para muchos, no más pequeñas que la longitud de Planck, que cuando explicamos le dimos un valor diminuto:
Así pues, las partículas tendrían forma de cuerda y si no las apreciamos como tal podría ser porque, como sucede con las aspas de un helicóptero, oscilan con tanta fuerza que apenas se ven. La analogía con las cuerdas de una guitarra no solo resulta útil sino que además es la mejor referencia. Cuando tocamos una cuerda muy fuertemente durante una fracción de segundo se hace más complicada de ver. Sería el mismo efecto pero con una cuerda más pequeña y más fina.
Las distintas formas de vibrar de la cuerda serían distintas «notas» de la misma, y cada nota daría lugar a fenómenos que nosotros asociaríamos a partículas diferentes.
Las notas de las cuerdas abiertas:
Como ya demostramos, las cuerdas abiertas cuantizadas dan lugar a un espectro cuántico de la siguiente forma:
Aquí ψ denota el estado cuántico, p el cuadrimomento de la cuerda, anI los operadores de creación de vibraciones con la nota n en la dirección I y λnI cuántas vibraciones se han creado del tipo asociado. En el número de dimensiones de oscilación fijamos como máximo 25, de forma acorde a nuestros cálculos.
Cada uno de estos estados cuánticos tendría una masa relativista asociada a la norma de su cuadrimomento y que en coordenadas cono luz tendría la expresión:
Ahora bien, carece de sentido necesitar el cuadrimomento de una cuerda para poder identificar su masa asociada. Hay otra forma más sencilla de calcularla, y pasa por recordar la definición del operador de Virasoro fundamental L0:
Aquí T sería la tensión de la cuerda y N el operador número: la nota que está tocando. Si N fuese nulo tendríamos la nota 0, donde la cuerda no está sonando: se mantiene rígida, si N fuese 1 la cuerda estaría tocando su primera nota…
De la última igualdad se puede despejar la siguiente relación muy importante:
Y sustituyendo en la expresión de la masa se obtiene:
Con esto tenemos más que suficiente para sacar conclusiones.
.-La nota 0: el taquión:
Si fijamos que N sea igual a 0, la cuerda no oscila en absoluto y su estado cuántico simplemente es el que fija su cuadrimomento:
Esto significa que la cuerda se manifestará como una partícula sin espín (escalar), cuya masa podemos calcular usando la ecuación obtenida:
¡Una masa que elevada al cuadrado es negativa! La partícula generada por la cuerda, necesariamente, debe estar moviéndose a velocidades superiores a la de la luz, y a dichas partículas tradicionalmente se las está denominando taquiones, un nombre inspirado en la palabra griega para decir «veloz».
Dado que los taquiones son escalares, cumplen con la ecuación de Klein-Gordon:
.-La nota 1: el fotón:
Supongamos ahora que fijamos N igual a 1. En estas circunstancias la cuerda generará estados cuánticos del siguiente modo:
 Aquí ξ es un espinor, un objeto que indica cuántas veces aparece un operador de creación en cada dirección. Para garantizar que la cuerda toque la primera nota, es necesario que todos sus valores sean fraccionarios y que la suma de oscilaciones fraccionadas en cada dirección de exactamente 1. Es decir: estamos repartiendo la primera nota entre todas las direcciones posibles, del mismo modo que cuando movemos la cuerda de una guitarra puede vibrar no solo en dos direcciones sino en cualquier dirección perpendicular a sí misma.
Aquí ξ es un espinor, un objeto que indica cuántas veces aparece un operador de creación en cada dirección. Para garantizar que la cuerda toque la primera nota, es necesario que todos sus valores sean fraccionarios y que la suma de oscilaciones fraccionadas en cada dirección de exactamente 1. Es decir: estamos repartiendo la primera nota entre todas las direcciones posibles, del mismo modo que cuando movemos la cuerda de una guitarra puede vibrar no solo en dos direcciones sino en cualquier dirección perpendicular a sí misma.
La ecuación obtenida, por otra parte, es idéntica a la que obtuvimos al cuantizar el campo electromagnético, con lo que todo apunta a que la cuerda estaría reproduciendo fotones. Esta sospecha toma más fuerza si comprobamos que en efecto su masa es nula:
Y se refuerza todavía más si vemos que el estado cuántico cumple la misma ecuación de movimiento que tenía que cumplir el campo electromagnético:
Fascinante, ¿no? Hemos reproducido la estructura matemática de una de las interacciones fundamentales de la naturaleza jugando con cuerdas abiertas vibrando.
Si seguimos avanzando en notas no veremos nada conocido, así que ha llegado la hora de pasar a la cuerda cerrada.
Las notas de las cuerdas cerradas:
Los estados cuánticos generados por estas tenían el siguiente aspecto:
El segundo paréntesis era debido a que en una cuerda cerrada podían inducirse oscilaciones en los dos sentidos y cada tipo tenía que analizarse por separado. Ahora bien, habíamos calculado también que afortunadamente las notas en una y otra dirección tenían que coincidir exactamente:
En esta ocasión, el operador de Virasoro variaba un poco, estando algunos términos divididos por 4 con respecto a la cuerda abierta:
De donde se despeja lo siguiente:
Dando lugar a la siguiente masa para los estados de la cuerda cerrada:
Aquí se aprecia muy fácilmente que es el resultado de la cuerda abierta multiplicado por 4. No obstante, no suele gustar esta expresión y es frecuente encontrar escrita la siguiente:
La diferencia fundamental es que esta segunda no da por hecho que las dos N sean iguales. Pero como en el caso que nos ocupa hemos calculado que sí lo son es más razonable emplear la expresión de arriba.
Y sin más demora, vayamos con las notas de la cuerda cerrada.
.-La nota 0: otro taquión:
Si la cuerda está rígida, de nuevo obtenemos un estado cuántico sin vibraciones, y la única diferencia con respecto a la cuerda abierta es que este taquión tiene una masa al cuadrado, ¡menuda sorpresa!, 4 veces más negativa:
Por lo demás, no hay otras consideraciones que interese hacer en este punto.
.-Las notas 1:
Consideremos ahora que fijamos N igual a 1 en una dirección. También será 1 en la dirección contraria, con lo que habrá dos ondas de la misma frecuencia propagándose sobre la cuerda cerrada dando lugar a una onda estacionaria con nodos y vientes fijos.
Su estado cuántico será:
Donde nos ha surgido un espinor ξ de dos índices.
La masa de este estado será nula en cualquier caso, como sucedía con la cuerda abierta. Sin embargo, no corresponde a una partícula clara solo por esa característica. De hecho, se corresponde con tres tipos de partículas diferentes.
Para diferenciarlas, podemos empezar separando el espinor en su parte simétrica y su parte antisimétrica:
Y una vez hecho esto, denotando por ξ su traza, podemos restársela y sumársela a su parte simétrica dividida entre el número de direcciones de oscilación:
Una vez hecho esto, ya tenemos separadas las tres partes de interés que dan lugar a tres tipos de partículas diferentes.
.–Gravitón:
Como vimos, los gravitones eran partículas sin masa con un espinor simétrico y de traza nula, así que se corresponderían con la parte entre paréntesis de la última ecuación. Sus ecuaciones de estado y de movimiento resultantes tendrían la forma:
De modo que las cuerdas cerradas son capaces de reproducir el campo gravitatorio, tal y como anticipamos. Esta es a día de hoy la única teoría cuántica de la gravedad con una analogía tan perfecta.
.–Partícula de Kalb-Ramond:
Si nos quedamos con la parte antisimetrizada, por su parte, obtenemos otras partículas diferentes que no aparecen ni de lejos en el Modelo Estándar y a las cuales se las tendría que denominar partículas de Kalb-Ramond, en honor a quienes hablaron por primera vez sobre su presencia y propiedades importantes en la teoría de cuerdas. Sus ecuaciones de estado y movimiento serían análogas:
.–Dilatón:
Por último, al quedarnos con el término de traza y usar la delta de Kronecker para cargarnos un sumatorio, obtenemos un campo escalar de masa nula que en torno a 1920 ya había aparecido en la teoría gravitatoria de Kaluza-Klein y al cuyas partículas se las denomina dilatones. Sus ecuaciones son:
Nótese que su ecuación de movimiento es la de Klein-Gordon, por lo que es un campo escalar.
Problemáticas evidentes:
La teoría de cuerdas, pese a reproducir perfectamente los gravitones, acabó siendo abandonada a mediados de los setenta por sus diversos inconvenientes: el exceso de dimensiones necesarias, su necesidad de enredar conceptos matemáticos como la convergencia de series y la presencia de taquiones: partículas que nunca han sido observadas ni se cree que existan.
Una teoría de cuerdas sin taquiones sería fantástica, pero en principio ello implicaría que las cuerdas nunca pudieran quedarse quietas y… ¿qué seriedad tendría una teoría del universo en la que sus ingredientes no tuviesen sentido al encontrarse en reposo?
Problemática no evidente:
Las cuerdas requerían de 25 dimensiones espaciales por cuestiones de su estructura matemática. Dicha necesidad se es manifiesta cada vez que las cuerdas quieran realizar acciones sencillas como interaccionar entre ellas o fragmentarse. La conclusión de ello es evidente: las cuerdas serían incompatibles donde hubiese algo que no fuesen cuerdas porque no podría haber contacto o nada tendría sentido.
Como consecuencia, la teoría de cuerdas es una teoría de todo o nada: o todo cuanto vemos está hecho de cuerdas o nada lo está.
Y esto resultó un golpe muy bajo, dado que estas cuerdas no reproducen ni electrones, ni neutrinos, ni quarks, ni nada que se les parezca. Podríamos pensar que igual dichas partículas se encuentran escondidas en notas más altas, pero la razón por la que no aparecen es muy sencilla y hace referencia al título de esta entrada: estas cuerdas solo reproducen bosones y nunca fermiones. Por eso son las cuerdas bosónicas.
¿Y por qué nunca producen fermiones? Porque los fermiones cumplen el principio de exclusión de Pauli, según el cual no pueden haber dos idénticos en el mismo estado simultáneamente. Y no hay nada que impida a estas cuerdas generar varias vibraciones idénticas en la misma dirección. Por tanto, hagan lo que hagan, solo reproducirán bosones.
Preludio a las super cuerdas:
Este último problema y el de los taquiones se arreglaron en los ochenta cuando se impuso que las cuerdas existiesen en espacios con propiedades geométricas diferentes, lo cual redujo el número de dimensiones espaciales necesarias a 9 además de cargarse los taquiones y permitir la aparición de fermiones entre las distintas notas. Pero hablaremos de esto más adelante. No tiene sentido hablar de super cuerdas sin haber mencionado nunca siquiera los ingredientes del Modelo Estándar en detalle.
Categorías:Física, Física cuántica, Partículas, Relatividad, Teoría de Cuerdas